【题目】若数列![]() 是公差为2的等差数列,数列
是公差为2的等差数列,数列![]() 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]()
对一切n∈N*恒成立,求实数λ的取值范围.
参考答案:
【答案】(1)![]() ;(2)(-2,3)。
;(2)(-2,3)。
【解析】
(1)对于anbn+bn=nbn+1.令n=1可求得a1=1,由等差数列的通项公式可求得an=2n-1。进而anbn+bn=nbn+1可变为2bn=bn+1,可得数列![]() 为等比数列,由等比数列的通项公式可求得bn=2n-1. (2)根据已知条件应先求得cn=
为等比数列,由等比数列的通项公式可求得bn=2n-1. (2)根据已知条件应先求得cn=![]() =
=![]() ,由特点根据错位相减法可求得Tn=4-
,由特点根据错位相减法可求得Tn=4-![]() .则不等式(-1)nλ<Tn+
.则不等式(-1)nλ<Tn+![]() ,化为(-1)nλ<4-
,化为(-1)nλ<4-![]() ,对n分奇数、偶数讨论,根据不等式恒成立可求实数λ的取值范围。
,对n分奇数、偶数讨论,根据不等式恒成立可求实数λ的取值范围。
(1) ∵数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1.
∴ n=1时,a1+1=2,解得a1=1.
又数列{an}是公差为2的等差数列,
∴an=1+2(n-1)=2n-1.
∴ 2nbn=nbn+1,化为2bn=bn+1,
∴数列{bn}是首项为1,公比为2的等比数列.
∴bn=2n-1.
(2)由数列{cn}满足cn=![]() =
=![]() =
=![]() ,数列{cn}的前n项和为
,数列{cn}的前n项和为
Tn=1+![]() +
+![]() +…+
+…+![]() ,
,
∴ ![]() Tn=
Tn=![]() +
+![]() +…+
+…+![]() +
+![]() ,
,
两式作差,得
∴![]() Tn=1+
Tn=1+![]() +
+![]() +…+
+…+![]() -
-![]() =
=![]() -
-![]() =2-
=2-![]() ,
,
∴Tn=4-![]() .
.
不等式(-1)nλ<Tn+![]() ,化为(-1)nλ<4-
,化为(-1)nλ<4-![]() ,
,
当n=2k(k∈N*)时,λ<4-![]() ,取n=2,
,取n=2,
∴λ<3.
当n=2k-1(k∈N*)时,-λ<4-![]() ,取n=1,
,取n=1,
∴λ>-2.
综上可得:实数λ的取值范围是(-2,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,内角A,B,C的对边分别是
 ,向量
,向量 ,且
,且 .
.(1)求角B的值;
(2)若
 ,且
,且 ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图所示的程序框图,若输入a的值为
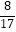 ,则输出的k值是( )
,则输出的k值是( ) 
A.9
B.10
C.11
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足a1=2,an+1=3an+2,
满足a1=2,an+1=3an+2, (1)证明:
 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式; (2)证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=2x3﹣3x2+
 ,则g(
,则g(  )+g(
)+g(  )+…+g(
)+…+g(  )=( )
)=( )
A.100
B.50
C.
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数
 在区间
在区间 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象
A. 向左平移
 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的 ,纵坐标不变
,纵坐标不变B. 向左平移至
 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变C. 向左平移
 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的 ,纵坐标不变
,纵坐标不变D. 向左平移
 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 -
科目: 来源: 题型:
查看答案和解析>>【题目】设m, n是两条不同的直线,
 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A.
 ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
相关试题

