【题目】在△ABC中,内角A,B,C的对边分别是![]() ,向量
,向量![]() ,且
,且![]() .
.
(1)求角B的值;
(2)若![]() ,且
,且![]() ,求△ABC的面积.
,求△ABC的面积.
参考答案:
【答案】(1)![]() ;(2)△ABC的面积为
;(2)△ABC的面积为![]() 。
。
【解析】
(1)由向量数量积的坐标运算可将m·n=bcos B化为![]() cos C+
cos C+![]() cos A=bcos B,然后用正弦定理的结论边化角可得 sin Acos C+sin Ccos A=2sin Bcos B,进而再用两角和正弦公式和诱导公式可求cos B=
cos A=bcos B,然后用正弦定理的结论边化角可得 sin Acos C+sin Ccos A=2sin Bcos B,进而再用两角和正弦公式和诱导公式可求cos B=![]() ,进而可求角B。(2)由(1)知B=
,进而可求角B。(2)由(1)知B=![]() ,可将cos
,可将cos![]() =
=![]() sin A中的角C化为A,可得cos
sin A中的角C化为A,可得cos![]() =
=![]() sin A。利用两角差的余弦公式可得tan A=
sin A。利用两角差的余弦公式可得tan A=![]() ,求得A=
,求得A=![]() ,进而求得C=
,进而求得C=![]() .由|m|=
.由|m|=![]() 可得即a2+c2=20,在直角三角形中,可得a=
可得即a2+c2=20,在直角三角形中,可得a=![]() c,进而可求a,c的值。可求结论。
c,进而可求a,c的值。可求结论。
(1) 由m·n=bcos B,得![]() cos C+
cos C+![]() cos A=bcos B,
cos A=bcos B,
sin Acos C+sin Ccos A=2sin Bcos B,
即 sin(A+C)=2sin Bcos B,sin B=2sin Bcos B,
∵0<B<π,sin B≠0,
∴cos B=![]() ,
,
∴B=![]() .
.
(2) C=π-A-B=![]() -A,cos
-A,cos![]() =
=![]() sin A
sin A
∴cos![]() =
=![]() sin A
sin A
∴cos A=![]() sin Atan A=
sin Atan A=![]()
∵ 0<A<![]() π,
π,
∴A=![]() ,
,
∴C=π-![]() -
-![]() =
=![]() .
.
在Rt△ABC中,a=csin![]() =
=![]() c,
c,
又|m|=![]() ,即a2+c2=20,
,即a2+c2=20,
∴a=2,c=4,b=![]() =2
=2![]() ,
,
△ABC的面积S=![]() ×2×2
×2×2![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解关于x的不等式:(a+1)x2-(2a+3)x+2<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前n项和Sn=n2+n .
的前n项和Sn=n2+n . (1)求数列
 的通项公式an;
的通项公式an;(2)令
 ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 )的部分图象如图所示,若将f(x)图象上的所有点向右平移
)的部分图象如图所示,若将f(x)图象上的所有点向右平移  个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( ) 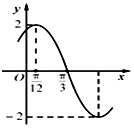
A.[kπ﹣ ,kπ+
,kπ+  ],k∈Z
],k∈Z
B.[2kπ﹣ ,2kπ+
,2kπ+  ],k∈Z
],k∈Z
C.[kπ﹣ ,kπ+
,kπ+  ],k∈Z
],k∈Z
D.[2kπ﹣ ,2kπ+
,2kπ+  ],k∈Z
],k∈Z -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图所示的程序框图,若输入a的值为
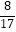 ,则输出的k值是( )
,则输出的k值是( ) 
A.9
B.10
C.11
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足a1=2,an+1=3an+2,
满足a1=2,an+1=3an+2, (1)证明:
 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式; (2)证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
 是公差为2的等差数列,数列
是公差为2的等差数列,数列 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)设数列
 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,若不等式
,若不等式
对一切n∈N*恒成立,求实数λ的取值范围.
相关试题

