【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则下列命题:
,则下列命题:
①对任意![]() ,都有
,都有![]() ;②函数
;②函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
③函数![]() 的最大值是1,最小值是0;④当
的最大值是1,最小值是0;④当![]() 时,
时,![]() .
.
其中正确命题的序号有________.
参考答案:
【答案】①②④
【解析】
根据已知,分析出函数的周期性,单调性,最值,函数解析式,逐一分析四个命题的真假,可得答案.
①∵![]() ,∴f(x+2)=f[(x+1)-1]=f(x),∴2是函数f(x)的一个周期,正确;②当
,∴f(x+2)=f[(x+1)-1]=f(x),∴2是函数f(x)的一个周期,正确;②当![]() 时,
时,![]() 为增函数,故x∈[-1,0]时,f(x)为减函数,由函数的周期性可得f(x)在(1,2)上是减函数,在(2,3)上是增函数,正确;③由解析式可知函数取最小值
为增函数,故x∈[-1,0]时,f(x)为减函数,由函数的周期性可得f(x)在(1,2)上是减函数,在(2,3)上是增函数,正确;③由解析式可知函数取最小值![]() ,取最大值1,故错误;④设x∈(3,4),则4-x∈(0,1),f(4-x)=
,取最大值1,故错误;④设x∈(3,4),则4-x∈(0,1),f(4-x)=![]() =f(-x)=f(x),故正确;
=f(-x)=f(x),故正确;
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
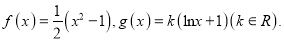
(Ⅰ)若
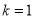 ,求
,求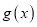 在
在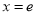 处的切线方程;
处的切线方程;(Ⅱ)证明:对任意正数
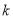 ,函数
,函数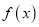 和
和 的图像总有两个公共点.
的图像总有两个公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三棱柱
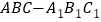 的高为2,
的高为2,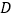 是
是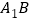 的中点,
的中点,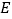 是
是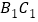 的中点
的中点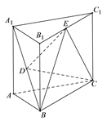
(1)证明:
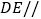 平面
平面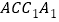 ;
;(2)若三棱锥
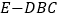 的体积为
的体积为 ,求该正三棱柱的底面边长.
,求该正三棱柱的底面边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
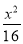 +
+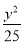 =1的焦点分别是
=1的焦点分别是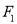 、
、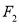 ,
, 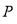 是椭圆上一点,若连结
是椭圆上一点,若连结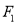 、
、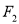 、
、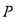 三点恰好能构成直角三角形,则点
三点恰好能构成直角三角形,则点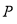 到
到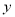 轴的距离是( )
轴的距离是( )A.
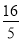 B.
B. 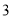 C.
C. 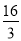 D.
D. 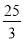
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆C1:
 +y2=1,椭圆C2:
+y2=1,椭圆C2:  (a>b>0)的一个焦点坐标为(
(a>b>0)的一个焦点坐标为(  ,0),斜率为1的直线l与椭圆C2相交于A、B两点,线段AB的中点H的坐标为(2,﹣1).
,0),斜率为1的直线l与椭圆C2相交于A、B两点,线段AB的中点H的坐标为(2,﹣1).
(1)求椭圆C2的方程;
(2)设P为椭圆C2上一点,点M、N在椭圆C1上,且 ,则直线OM与直线ON的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由.
,则直线OM与直线ON的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
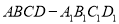 中,点
中,点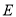 是棱
是棱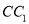 上的一个动点,平面
上的一个动点,平面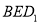 交棱
交棱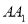 于点
于点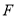 .给出下列命题:
.给出下列命题: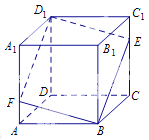
①存在点
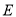 ,使得
,使得 //平面
//平面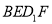 ;
;②对于任意的点
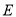 ,平面
,平面 平面
平面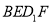 ;
;③存在点
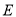 ,使得
,使得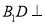 平面
平面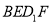 ;
;④对于任意的点
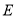 ,四棱锥
,四棱锥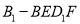 的体积均不变.
的体积均不变.其中正确命题的序号是______.(写出所有正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
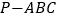 中,
中,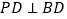 ,
,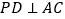 ,
,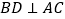 ,且
,且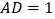 ,
,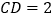 ,
,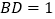 ,
,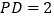 ,
,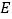 为
为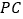 上一点,
上一点,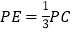 .
.(1)求证:
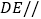 平面
平面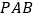 ;
;(2)求异面直线
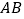 和
和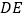 所成角的余弦值.
所成角的余弦值.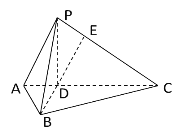
相关试题

