【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.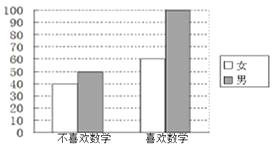
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
参考答案:
【答案】
(1)100;60;160;50;40;90;150;100;250
(2)
解: ![]()
所以有60%的把握认为“性别与喜欢数学有关系”.
【解析】本题主要考查了独立性检验的应用,解决问题的关键是(1)根据所给的二维条形图看出喜欢数学课程和不喜欢数学课程的学生数,得到列联表;(2)把列联表中的数据代入求观测值的公式,求出这组数据的观测值,把观测值同临界值进行比较,得到有60%的把握认为“性别与喜欢数学有关系”
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病
不患三高疾病
合计
男
6
30
女
合计
36
下面的临界值表供参考:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
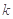
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式
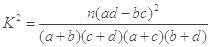 ,其中
,其中 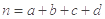 )
)
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽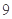 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量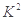 ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关? -
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,值域为(0,+∞)的函数是( )
A.y=5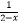
B.y=log2(3x+2)
C.y=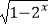
D.y=( )1﹣x
)1﹣x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log3(ax2+3x+4)
(1)若f(1)<2,求a的取值范围
(2)若a=1,求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】
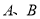 两城相距
两城相距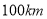 ,在两城之间距
,在两城之间距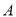 城
城 处建一核电站给
处建一核电站给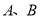 两城供电,为保证城市安全,核电站距城市距离不得小于
两城供电,为保证城市安全,核电站距城市距离不得小于 .已知供电费用等于供电距离
.已知供电费用等于供电距离 的平方与供电量(亿度)之积的
的平方与供电量(亿度)之积的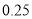 倍,若
倍,若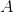 城供电量为每月20亿度,城供电量为每月10亿度.
城供电量为每月20亿度,城供电量为每月10亿度.(1)把月供电总费用
 表示成
表示成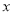 的函数;
的函数;(2)核电站建在距
 城多远,才能使供电总费用
城多远,才能使供电总费用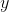 最少?
最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =
 ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.
相关试题

