【题目】已知函数f(x)=log3(ax2+3x+4)
(1)若f(1)<2,求a的取值范围
(2)若a=1,求函数f(x)的值域.
参考答案:
【答案】
(1)解:∵f(1)<2,
∴log3(a+7)<2=log39,
∴0<a+7<9,
解得:﹣7<a<2
(2)解:若a=1,函数f(x)=log3(x2+3x+4)
x2+3x+4≥ ![]() ,且y=log3t为增函数,
,且y=log3t为增函数,
故f(x)≥log3 ![]() ,
,
∴函数f(x)的值域为[log3 ![]() ,+∞)
,+∞)
【解析】(1)若f(1)<2,则log3(a+7)<2,解得a的取值范围(2)若a=1,则f(x)=log3(x2+3x+4),由二次函数的图象和性质,求出真数的范围,进而可得函数f(x)的值域.
【考点精析】通过灵活运用函数的值域和函数的最值及其几何意义,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,值域为(0,+∞)的函数是( )
A.y=5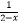
B.y=log2(3x+2)
C.y=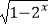
D.y=( )1﹣x
)1﹣x -
科目: 来源: 题型:
查看答案和解析>>【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
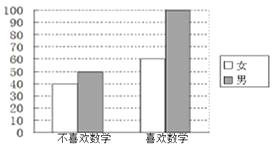
(1)根据二维条形图,完成下表:男
女
合计
喜欢数学课程
不喜欢数学课程
合计
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”? -
科目: 来源: 题型:
查看答案和解析>>【题目】
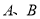 两城相距
两城相距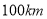 ,在两城之间距
,在两城之间距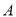 城
城 处建一核电站给
处建一核电站给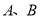 两城供电,为保证城市安全,核电站距城市距离不得小于
两城供电,为保证城市安全,核电站距城市距离不得小于 .已知供电费用等于供电距离
.已知供电费用等于供电距离 的平方与供电量(亿度)之积的
的平方与供电量(亿度)之积的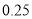 倍,若
倍,若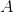 城供电量为每月20亿度,城供电量为每月10亿度.
城供电量为每月20亿度,城供电量为每月10亿度.(1)把月供电总费用
 表示成
表示成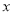 的函数;
的函数;(2)核电站建在距
 城多远,才能使供电总费用
城多远,才能使供电总费用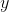 最少?
最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =
 ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+2)=f(x﹣2),且当x∈[﹣2,0]时,f(x)=(
 )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)有3个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)有3个不同的实数根,则a的取值范围是( )
A.(1,2)
B.(2,+∞)
C.(1,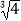 )
)
D.(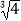 ,2)
,2)
相关试题

