【题目】已知动点![]() 到点
到点![]() 和直线l:
和直线l: ![]() 的距离相等.
的距离相等.
(Ⅰ)求动点![]() 的轨迹E的方程;
的轨迹E的方程;
(Ⅱ)已知不与![]() 垂直的直线
垂直的直线![]() 与曲线E有唯一公共点A,且与直线
与曲线E有唯一公共点A,且与直线![]() 的交点为
的交点为![]() ,以AP为直径作圆
,以AP为直径作圆![]() .判断点
.判断点![]() 和圆
和圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)根据抛物线定义可得方程(2)以AP为直径作圆![]() ,判断点
,判断点![]() 和圆
和圆![]() 的位置关系则只需验证
的位置关系则只需验证![]() 等于零否从而可得结论
等于零否从而可得结论
(Ⅰ)设动点![]() ,
,
由抛物线定义可知点![]() 的轨迹E是以
的轨迹E是以![]() 为焦点,直线l:
为焦点,直线l: ![]() 为准线的抛物线,
为准线的抛物线,
所以轨迹E的方程为![]() .
.
(Ⅱ)法1:由题意可设直线![]() ,
,
由![]() 可得
可得![]() (*),
(*),
因为直线![]() 与曲线E有唯一公共点A,
与曲线E有唯一公共点A,
所以![]() ,即
,即![]() .
.
所以(*)可化简为![]() ,
,
所以![]() ,
,
令![]() 得
得![]() ,
,
因为![]() ,
,
所以![]()
所以![]() ,
,
所以点![]() 在以PA为直径的圆
在以PA为直径的圆![]() 上.
上.
法2:依题意可设直线![]() ,
,
由![]() 可得
可得![]() (*),
(*),
因为直线![]() 与曲线E有唯一公共点A,且与直线
与曲线E有唯一公共点A,且与直线![]() 的交点为
的交点为![]() ,
,
所以![]() 即
即![]()
所以(*)可化简为![]() ,
,
所以![]() .
.
令![]() 得
得![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以点![]() 在以PA为直径的圆
在以PA为直径的圆![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (x∈R),e是自然对数的底.
(x∈R),e是自然对数的底.
(1)计算f(ln2)的值;
(2)证明函数f(x)是奇函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥
 ,侧棱
,侧棱 ,底面三角形
,底面三角形 为正三角形,边长为
为正三角形,边长为 ,顶点
,顶点 在平面
在平面 上的射影为
上的射影为 ,有
,有 ,且
,且 .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值;
的余弦值;(Ⅲ)线段
 上是否存在点
上是否存在点 使得
使得 ⊥平面
⊥平面 ,如果存在,求
,如果存在,求 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选择意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.

上图中,已知课程
 为人文类课程,课程
为人文类课程,课程 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取 的学生作为研究样本组(以下简称“组M”).
的学生作为研究样本组(以下简称“组M”).(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)为参加某地举办的自然科学营活动,从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往,其中选择课程F或课程H的同学参加本次活动,费用为每人1500元,选择课程G的同学参加,费用为每人2000元.
(ⅰ)设随机变量
 表示选出的4名同学中选择课程
表示选出的4名同学中选择课程 的人数,求随机变量
的人数,求随机变量 的分布列;
的分布列;(ⅱ)设随机变量
 表示选出的4名同学参加科学营的费用总和,求随机变量
表示选出的4名同学参加科学营的费用总和,求随机变量 的期望.
的期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={1,2,3},集合B={x|a+1<x<6a﹣1},其中a∈R.
(1)写出集合A的所有真子集;
(2)若A∩B={3},求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于无穷数列
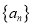 ,记
,记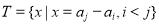 ,若数列
,若数列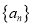 满足:“存在
满足:“存在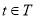 ,使得只要
,使得只要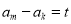 (
(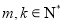 且
且 ),必有
),必有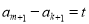 ”,则称数列
”,则称数列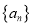 具有性质
具有性质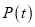 .
.(Ⅰ)若数列
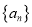 满足
满足 判断数列
判断数列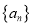 是否具有性质
是否具有性质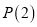 ?是否具有性质
?是否具有性质 ?
?(Ⅱ)求证:“
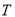 是有限集”是“数列
是有限集”是“数列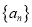 具有性质
具有性质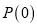 ”的必要不充分条件;
”的必要不充分条件;(Ⅲ)已知
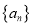 是各项为正整数的数列,且
是各项为正整数的数列,且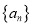 既具有性质
既具有性质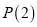 ,又具有性质
,又具有性质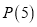 ,求证:存在整数
,求证:存在整数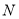 ,使得
,使得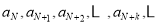 是等差数列.
是等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
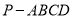 的底面是边长为
的底面是边长为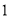 的正方形,
的正方形, 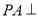 底面
底面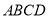 ,
, 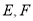 分别为
分别为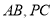 的中点.
的中点.(Ⅰ)求证:
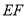
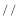 平面
平面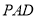 ;
;(Ⅱ)若
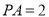 ,试问在线段
,试问在线段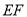 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 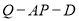 的余弦值为
的余弦值为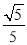 ?若存在,确定点
?若存在,确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.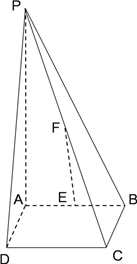
相关试题

