【题目】已知函数![]() 的图象如图所示.
的图象如图所示.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅲ)在(Ⅱ)的条件下,函数![]() 与
与![]() 的图象有三个不同的交点,求
的图象有三个不同的交点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】试题分析:(I)由图可知函数![]() 的图象过点(0,3),即
的图象过点(0,3),即![]() ,且
,且![]() ,由此列方程组可求得
,由此列方程组可求得![]() .(II)由(I)知
.(II)由(I)知![]() ,将
,将![]() 代入切线方程,求得切点坐标为
代入切线方程,求得切点坐标为![]() ,即
,即![]() ,且切线的斜率为
,且切线的斜率为![]() ,即
,即![]() ,由此建立方程组,求得
,由此建立方程组,求得![]() .(III)由(II)知
.(III)由(II)知![]() .将原问题转化为:
.将原问题转化为: ![]() 有三个不等实根,即:
有三个不等实根,即: ![]() 与
与![]() 轴有三个交点,只需要其极大值大于零,极小值小于零,利用导数求出
轴有三个交点,只需要其极大值大于零,极小值小于零,利用导数求出![]() 的极值,列不等组即可求得
的极值,列不等组即可求得![]() 的取值范围.
的取值范围.
试题解析:
函数![]() 的导函数为
的导函数为![]()
(Ⅰ)由图可知函数![]() 的图象过点(0,3),且
的图象过点(0,3),且![]()
得 ![]()
(Ⅱ)依题意 ![]() 且
且![]()
![]()
解得 ![]()
所以![]()
(Ⅲ)![]() .可转化为:
.可转化为: ![]() 有三个不等实根,即:
有三个不等实根,即: ![]() 与
与![]() 轴有三个交点;
轴有三个交点;
![]() ,
,
|
|
|
|
|
|
|
| 0 | - | 0 |
|
| 增 | 极大值 | 减 | 极小值 | 增 |
![]() .当且仅当
.当且仅当![]() 时,有三个交点,
时,有三个交点,
故而, ![]() 为所求.
为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先后2次抛掷一枚骰子,将得到的点数分别记为
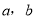 .
.(Ⅰ)求满足
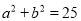 的概率;
的概率;(Ⅱ)设三条线段的长分别为
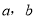 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,
, 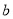 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;(2)若
 ,
,  都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的方程
的方程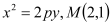 为抛物线
为抛物线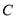 上一点,
上一点,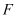 为抛物线的焦点.
为抛物线的焦点.(I)求
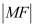 ;
;(II)设直线
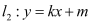 与抛物线
与抛物线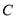 有唯一公共点
有唯一公共点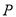 ,且与直线
,且与直线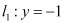 相交于点
相交于点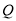 ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点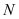 ,使得以
,使得以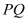 为直径的圆恒过点
为直径的圆恒过点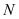 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一名学生每天骑车上学,从他家里到学校的途中有6个交通岗,假设在每个交通岗遇到红灯的事件是相互独立的,并且概率都是
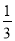 .
.(1)假设
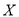 为这名学生在途中遇到红灯的次数,求
为这名学生在途中遇到红灯的次数,求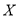 的分布列;
的分布列;(2)设
 为这名学生在首次停车前经过的路口数,求
为这名学生在首次停车前经过的路口数,求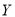 的分布列;
的分布列; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
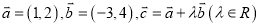 .
.(1)当
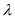 为何值时,
为何值时, 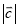 最小? 此时
最小? 此时 与
与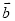 的位置关系如何?
的位置关系如何?(2)当
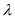 为何值时,
为何值时, 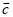 与
与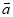 的夹角最小? 此时
的夹角最小? 此时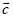 与
与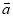 的位置关系如何?
的位置关系如何?
相关试题

