【题目】正方体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上求一点
上求一点![]() ,使得
,使得![]() 平面
平面![]() .
.
参考答案:
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)以D为原点,DA,DC,D![]() 分别为x,y,z轴建立空间直角坐标系,
分别为x,y,z轴建立空间直角坐标系,
只需证明两平面的法向量数量积为0.(2)设![]() ,解得M(2,2λ,λ),由
,解得M(2,2λ,λ),由![]() 平面
平面![]() ,需
,需![]() ,可求解。
,可求解。
试题解析: 证明:(Ⅰ)建立如图所示的空间直角坐标系D-xyz,
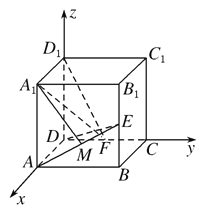
不妨设正方体的棱长为2,则A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2), D1(0,0,2).
设平面AED的法向量为n1=(x1,y1,z1),则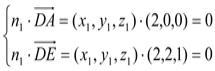
∴![]()
令y1=1,得n1=(0,1,-2).
同理可得平面A1FD1的法向量n2=(0,2,1).
∵n1·n2=0,
∴平面AED⊥平面A1FD1.
(Ⅱ)由于点M在AE上,
∴可设![]() =λ
=λ![]() =λ(0,2,1)=(0,2λ,λ),
=λ(0,2,1)=(0,2λ,λ),
可得M(2,2λ,λ),
于是![]() =(0,2λ,λ-2).
=(0,2λ,λ-2).
要使A1M⊥平面DAE,需A1M⊥AE,
∴![]() ·
·![]() =(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=
=(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=![]() .
.
故当AM=![]() AE时,即点M坐标为(2,
AE时,即点M坐标为(2,![]() ,
,![]() )时,A1M⊥平面DAE.
)时,A1M⊥平面DAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中, ,
, ,
,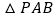 和
和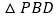 都是边长为2的等边三角形,设
都是边长为2的等边三角形,设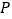 在底面
在底面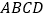 的射影为
的射影为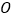 .
.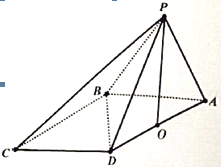
(1)求证:
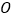 是
是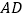 中点;
中点;(2)证明:
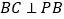 ;
;(3)求二面角
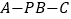 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市公租房的房源位于
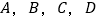 四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:(1)求恰有1人申请
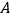 片区房源的概率;
片区房源的概率;(2)用
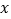 表示选择
表示选择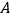 片区的人数,求
片区的人数,求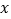 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2014课标全国Ⅰ,文12】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修
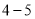 :不等式选讲
:不等式选讲已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2015高考天津,文20】已知函数
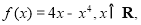
(I)求
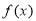 的单调区间;
的单调区间;(II)设曲线
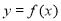 与
与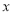 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为 ,求证:对于任意的正实数
,求证:对于任意的正实数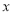 ,都有
,都有 ;
;(III)若方程
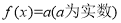 有两个正实数根
有两个正实数根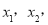 且
且 ,求证:
,求证: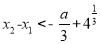 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为
 ,乙能攻克的概率为
,乙能攻克的概率为 ,丙能攻克的概率为
,丙能攻克的概率为 .
.(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励
 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金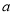 万元;若只有2人攻克,则奖金奖给此二人,每人各得
万元;若只有2人攻克,则奖金奖给此二人,每人各得 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
相关试题

