【题目】【2015高考天津,文20】已知函数![]()
(I)求![]() 的单调区间;
的单调区间;
(II)设曲线![]() 与
与![]() 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为![]() ,求证:对于任意的正实数
,求证:对于任意的正实数![]() ,都有
,都有![]() ;
;
(III)若方程![]() 有两个正实数根
有两个正实数根![]() 且
且![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(I)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(II)见试题解析;(III)见试题解析.
;(II)见试题解析;(III)见试题解析.
【解析】
(I)由![]() ,可得
,可得![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(II)
;(II)![]() ,
,![]() ,证明
,证明![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,所以对任意的实数x,
单调递减,所以对任意的实数x,![]() ,对于任意的正实数
,对于任意的正实数![]() ,都有
,都有![]() ;(III)设方程
;(III)设方程![]() 的根为
的根为![]() ,可得
,可得![]() ,由
,由![]() 在
在![]() 单调递减,得
单调递减,得![]() ,所以
,所以![]() .设曲线
.设曲线![]() 在原点处的切线为
在原点处的切线为![]() 方程
方程![]() 的根为
的根为![]() ,可得
,可得![]() ,由
,由![]() 在在
在在![]() 单调递增,且
单调递增,且![]() ,可得
,可得![]() 所以
所以![]() .
.
试题解析:(I)由![]() ,可得
,可得![]() ,当
,当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递增;当
单调递增;当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减.所以函数
单调递减.所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(II)设![]() ,则
,则![]() ,
,![]() 曲线
曲线![]() 在点P处的切线方程为
在点P处的切线方程为![]() ,即
,即![]() ,令
,令![]() 即
即![]() 则
则![]() .
.
由于![]() 在
在![]() 单调递减,故
单调递减,故![]() 在
在![]() 单调递减,又因为
单调递减,又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,所以对任意的实数x,
单调递减,所以对任意的实数x,![]() ,对于任意的正实数
,对于任意的正实数![]() ,都有
,都有![]() .
.
(III)由(II)知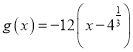 ,设方程
,设方程![]() 的根为
的根为![]() ,可得
,可得![]() ,因为
,因为![]() 在
在![]() 单调递减,又由(II)知
单调递减,又由(II)知![]() ,所以
,所以![]() .类似的,设曲线
.类似的,设曲线![]() 在原点处的切线为
在原点处的切线为![]() 可得
可得![]() ,对任意的
,对任意的![]() ,有
,有![]() 即
即![]() .设方程
.设方程![]() 的根为
的根为![]() ,可得
,可得![]() ,因为
,因为![]() 在
在![]() 单调递增,且
单调递增,且![]() ,因此,
,因此,![]() 所以
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2014课标全国Ⅰ,文12】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 中,
中,  分别是
分别是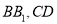 的中点.
的中点.(1)证明:平面
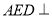 平面
平面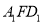 ;
;(2)在
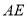 上求一点
上求一点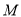 ,使得
,使得 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修
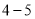 :不等式选讲
:不等式选讲已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为
 ,乙能攻克的概率为
,乙能攻克的概率为 ,丙能攻克的概率为
,丙能攻克的概率为 .
.(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励
 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金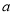 万元;若只有2人攻克,则奖金奖给此二人,每人各得
万元;若只有2人攻克,则奖金奖给此二人,每人各得 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分) -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
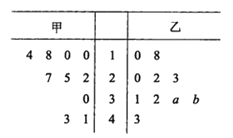
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当
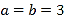 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为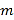 ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为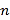 ,比较
,比较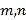 的大小关系;
的大小关系;(2)在这10个卖场中,随机选取2个卖场,记
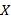 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求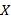 的分布列和数学期望;
的分布列和数学期望;(3)若
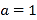 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为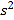 ,根据茎叶图推断
,根据茎叶图推断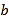 为何值时,
为何值时,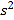 达到最小值.(只需写出结论)
达到最小值.(只需写出结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩掷骰子游戏,甲掷出的点数记为
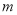 ,乙掷出的点数记为
,乙掷出的点数记为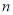 ,
,若关于
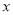 的一元二次方程
的一元二次方程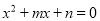 有两个不相等的实数根时甲胜;方程有
有两个不相等的实数根时甲胜;方程有两个相等的实数根时为“和”;方程没有实数根时乙胜.
(1)列出甲、乙两人“和”的各种情形;
(2)求甲胜的概率.
必要时可使用此表格

相关试题

