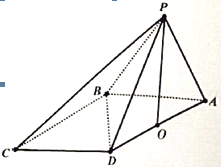
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 和
和![]() 都是边长为2的等边三角形,设
都是边长为2的等边三角形,设![]() 在底面
在底面![]() 的射影为
的射影为![]() .
.
(1)求证:![]() 是
是![]() 中点;
中点;
(2)证明:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】试题分析:(1)根据等边三角形有![]() ,依题意有
,依题意有![]() 平面
平面![]() ,故
,故![]() ,由此可知
,由此可知![]() 为
为![]() 中点.(2)由
中点.(2)由![]() 平面
平面![]() 可得
可得![]() ,而
,而![]() ,即
,即![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() .(3)以
.(3)以![]() 分别为
分别为![]() 轴建立空间直角坐标系,利用法向量计算二面角的余弦值.
轴建立空间直角坐标系,利用法向量计算二面角的余弦值.
试题解析:(1)证明:∵![]() 和
和![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,
又∵![]() 底面
底面![]() ,
,
∴![]() ,
,
则点![]() 为
为![]() 的外心,又因为
的外心,又因为![]() 是直角三角形,
是直角三角形,
∴点![]() 为
为![]() 中点.
中点.
(2)证明:由(1)知,点![]() 在底面的射影为点
在底面的射影为点![]() ,点
,点![]() 为
为![]() 中点,
中点,
于是![]() 面
面![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
从而![]() 即
即![]() ,
,
由![]() ,
,![]() 得
得![]() 面
面![]() ,
,
∴![]() .
.
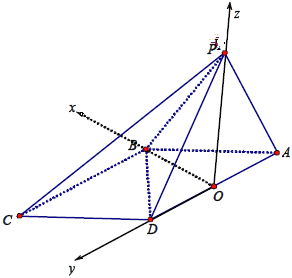
(3)以点![]() 为原点,以
为原点,以![]() 所在射线为
所在射线为![]() 轴 ,
轴 ,![]() 轴,
轴,![]() 轴建系如图,
轴建系如图,
∵![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
取![]() ,得
,得![]() ,
,![]() ,
,
故![]() .
.
设面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
取![]() ,则
,则![]() ,故
,故![]() ,
,
于是![]() ,
,
由图观察知![]() 为钝二面角,
为钝二面角,
所以该二面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l、m,平面α、β,下列命题正确的是 ( )
A. l∥β,lαα∥β
B. l∥β,m∥β,lα,mαα∥β
C. l∥m,lα,mβα∥β
D. l∥β,m∥β,lα,mα,l∩m=Mα∥β
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图所示,设E、F、E1、F1分别是长方体ABCD-A1B1C1D1的棱AB、CD、A1B1、C1D1的中点,则平面EFD1A1与平面BCF1E1的位置关系是 ( )

A. 平行 B. 相交 C. 异面 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公租房的房源位于
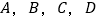 四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:(1)求恰有1人申请
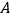 片区房源的概率;
片区房源的概率;(2)用
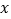 表示选择
表示选择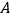 片区的人数,求
片区的人数,求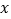 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2014课标全国Ⅰ,文12】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 中,
中,  分别是
分别是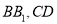 的中点.
的中点.(1)证明:平面
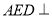 平面
平面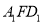 ;
;(2)在
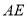 上求一点
上求一点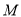 ,使得
,使得 平面
平面 .
.
相关试题

