【题目】某大学高等数学老师这学期分别用![]() 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:

(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() 其中
其中![]() )
)
参考答案:
【答案】(Ⅰ)甲班高等数学成绩集中于60-90分之间,而乙班数学成绩集中于80-100分之间,所以乙班的平均分高.
(Ⅱ)![]() ;
;
(Ⅲ)在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关。
【解析】
试题分析:(Ⅰ)甲班高等数学成绩集中于60-90分之间,而乙班数学成绩集中于80-100分之间,所以乙班的平均分高 3分
(Ⅱ)记成绩为86分的同学为![]() ,其他不低于80分的同学为
,其他不低于80分的同学为![]()
“从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有:
 一共15个,
一共15个,
“抽到至少有一个86分的同学”所组成的基本事件有:![]() 共9个, 5分
共9个, 5分
故![]() 7分
7分
(Ⅲ)
甲班 | 乙班 | 合计 | |
优秀 | 3 | 10 | 13 |
不优秀 | 17 | 10 | 27 |
合计 | 20 | 20 | 40 |
9分
![]() ,因此在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关。 12分
,因此在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关。 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①圆
 与直线
与直线 相交,所得弦长为
相交,所得弦长为 ;
;②直线
 与圆
与圆 恒有公共点;
恒有公共点;③若棱长为
 的正方体的顶点都在同一球面上,则该球的表面积为
的正方体的顶点都在同一球面上,则该球的表面积为 ;
;④若棱长为
 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为 .
.其中,正确命题的序号为__________.(写出所有正确命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资
 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.(1)分别写出
 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是公差不为0的等差数列,首项a1=1,且a1 , a2 , a4成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足bn=an+2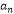 ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在椭圆
在椭圆 :
:  (
( )上,设
)上,设 ,
,  ,
,  分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点 到直线
到直线 的距离为
的距离为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设点
 ,
,  (
( )为椭圆
)为椭圆 上两点,且满足
上两点,且满足 ,求证:
,求证:  的面积为定值,并求出该定值.
的面积为定值,并求出该定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了探究某市高中理科生在高考志愿中报考“经济类”专业是否与性别有关,现从该市高三理科生中随机抽取50各学生进行调查,得到如下2×2列联表:(单位:人).
报考“经济类”
不报“经济类”
合计
男
6
24
30
女
14
6
20
合计
20
30
50
(Ⅰ)据此样本,能否有99%的把握认为理科生报考“经济类”专业与性别有关?
(Ⅱ)若以样本中各事件的频率作为概率估计全市总体考生的报考情况,现从该市的全体考生(人数众多)中随机抽取3人,设3人中报考“经济类”专业的人数为随机变量X,求随机变量X的概率分布及数学期望.
附:参考数据:P(X2≥k)
0.05
0.010
k
3.841
6.635
(参考公式:X2=
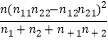 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点. (Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求二面角A﹣A1B﹣C1的大小.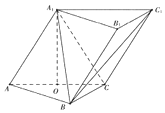
相关试题

