【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点. (Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求二面角A﹣A1B﹣C1的大小.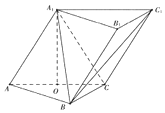
参考答案:
【答案】证明:(Ⅰ)∵AA1=A1C,且O为AC的中点, ∴A1O⊥AC,
又∵侧面AA1C1C⊥底面ABC,交线为AC,且A1O平面AA1C1C,
∴A1O⊥平面ABC
解:(Ⅱ)如图,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
由已知可得O(0,0,0),A(0,﹣1,0), ![]() ,
, ![]() ,
, ![]()
∴ ![]() ,
, ![]() ,
, ![]()
设平面AA1B的一个法向量为 ![]() ,
,
则有 
令x1=1,得 ![]() ,z1=1
,z1=1
∴ ![]()
设平面A1BC1的法向量为 ![]() ,
,
则有 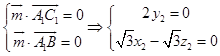
令x2=1,则y2=0,z2=1,∴ ![]()
∴ ![]()
∴所求二面角的大小为 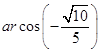
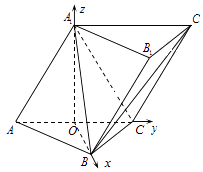
【解析】(Ⅰ)推导出A1O⊥AC,由此能证明A1O⊥平面ABC.(Ⅱ)以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出二面角A﹣A1B﹣C1的大小.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学高等数学老师这学期分别用
 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的
 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”甲班
乙班
合计
优秀
不优秀
合计
下面临界值表仅供参考:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
 其中
其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在椭圆
在椭圆 :
:  (
( )上,设
)上,设 ,
,  ,
,  分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点 到直线
到直线 的距离为
的距离为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设点
 ,
,  (
( )为椭圆
)为椭圆 上两点,且满足
上两点,且满足 ,求证:
,求证:  的面积为定值,并求出该定值.
的面积为定值,并求出该定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了探究某市高中理科生在高考志愿中报考“经济类”专业是否与性别有关,现从该市高三理科生中随机抽取50各学生进行调查,得到如下2×2列联表:(单位:人).
报考“经济类”
不报“经济类”
合计
男
6
24
30
女
14
6
20
合计
20
30
50
(Ⅰ)据此样本,能否有99%的把握认为理科生报考“经济类”专业与性别有关?
(Ⅱ)若以样本中各事件的频率作为概率估计全市总体考生的报考情况,现从该市的全体考生(人数众多)中随机抽取3人,设3人中报考“经济类”专业的人数为随机变量X,求随机变量X的概率分布及数学期望.
附:参考数据:P(X2≥k)
0.05
0.010
k
3.841
6.635
(参考公式:X2=
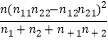 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意 ,恒有
,恒有 ;②对于定义域上的任意
;②对于定义域上的任意 .当
.当 ,恒有
,恒有 .则称函数
.则称函数 为“理想函数”,则下列三个函数中:
为“理想函数”,则下列三个函数中:(1)
 ,
,(2)
 ,
,(3)
 .
.称为“理想函数”的有 (填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生喜欢校内、校外开展活动的情况,某中学一课外活动小组在学校高一年级进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按
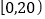 ,
,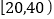 ,
,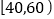 ,
,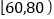 ,
,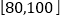 分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为
分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为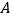 类学生,低于60分的称为
类学生,低于60分的称为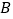 类学生.
类学生.
(1)根据已知条件完成下面
 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过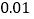 的前提下认为性别与是否为
的前提下认为性别与是否为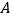 类学生有关系?
类学生有关系?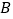 类
类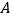 类
类合计
男
110
女
50
合计
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中
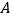 类学生的人数为
类学生的人数为 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求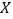 的分布列、期望
的分布列、期望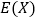 和方差
和方差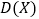 .
.参考公式:
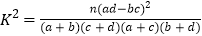 ,其中
,其中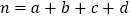 .
.参考临界值:
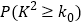
0.10
0.05
0.025
0.010
0.005
0.001
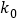
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
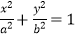 (a>b>0)的左焦点为F1(﹣
(a>b>0)的左焦点为F1(﹣ 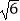 ,0),e=
,0),e= 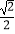 . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)如图,设R(x0 , y0)是椭圆C上一动点,由原点O向圆(x﹣x0)2+(y﹣y0)2=4引两条切线,分别交椭圆于点P,Q,若直线OP,OQ的斜率存在,并记为k1 , k2 , 求证:k1k2为定值;
(Ⅲ)在(Ⅱ)的条件下,试问OP2+OQ2是否为定值?若是,求出该值;若不是,说明理由.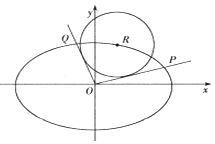
相关试题

