【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角
![]() 的余弦值.
的余弦值.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,先根据三角形中位线定理及平行四边形的性质可得
,先根据三角形中位线定理及平行四边形的性质可得![]() ,再证明
,再证明![]() 平面
平面![]() ,从而可得
,从而可得![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果
的一个法向量,根据空间向量夹角余弦公式,可得结果
试题解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() .
.
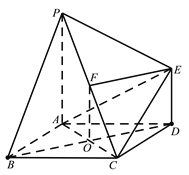
因为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
因为![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]() .
.
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是菱形,所以
是菱形,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解法:因为直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以![]() ,所以
,所以![]() .
.
 所以
所以 ![]() ,故△
,故△![]() 为等边三角形.
为等边三角形.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() .
.
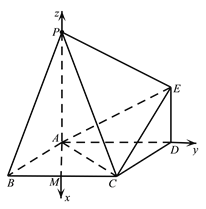
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() (如图).
(如图).
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 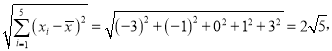 .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 即
即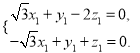
![]() 则
则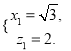 所以
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 即
即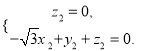 令
令![]() 则
则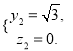 所以
所以![]() .
.
设二面角![]() 的大小为
的大小为![]() ,由于
,由于![]() 为钝角,
为钝角,
所以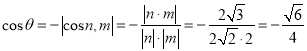 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直及面面垂直的判定定理以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.
-
科目: 来源: 题型:
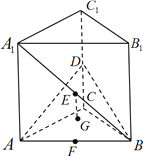
查看答案和解析>>【题目】如图,在直三棱柱
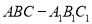 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, 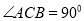 ,侧棱
,侧棱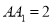 ,点
,点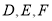 分别为棱
分别为棱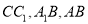 的中点,
的中点, 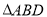 的重心为
的重心为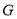 ,直线
,直线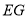 垂直于平面
垂直于平面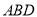 .
.
(1)求证:直线
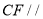 平面
平面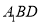 ;
;(2)求二面角
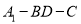 的余弦.
的余弦. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
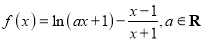 .
.(1)若
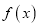 在
在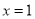 时取到极值,求
时取到极值,求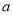 的值及
的值及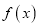 的图象在
的图象在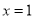 处的切线方程;
处的切线方程;(2)若
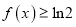 在
在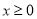 时恒成立,求
时恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以坐标原点
 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线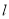 上两点
上两点 的极坐标分别为
的极坐标分别为 ,圆
,圆 的参数方程为
的参数方程为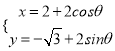 (
( 为参数).
为参数).(1)设
 为线段
为线段 的中点,求直线
的中点,求直线 的平面直角坐标方程;
的平面直角坐标方程;(2)判断直线
 与圆
与圆 的位置关系.
的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量
 (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量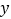 (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料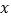 (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.
(1)依据数据的折线图,是否可用线性回归模型拟合
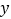 与
与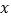 的关系?请计算相关系数
的关系?请计算相关系数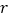 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若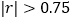 ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量
 限制,并有如下关系:
限制,并有如下关系:周光照量
 (单位:小时)
(单位:小时)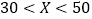

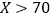
光照控制仪最多可运行台数
3
2
1
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.
附:相关系数公式
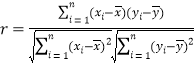 ,参考数据
,参考数据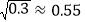 ,
,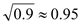 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
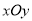 中,椭圆
中,椭圆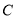 :
: 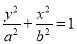
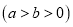 的上焦点为
的上焦点为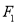 ,椭圆
,椭圆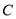 的离心率为
的离心率为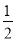 ,且过点
,且过点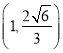 .
.(1)求椭圆
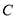 的方程;
的方程;(2)设过椭圆
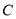 的上顶点
的上顶点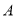 的直线
的直线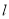 与椭圆
与椭圆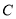 交于点
交于点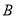 (
(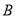 不在
不在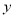 轴上),垂直于
轴上),垂直于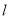 的直线与
的直线与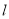 交于点
交于点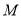 ,与
,与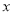 轴交于点
轴交于点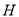 ,若
,若 ,且
,且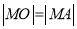 ,求直线
,求直线 的方程.
的方程.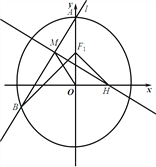
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
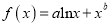
 .
.(1)当
 时,若函数
时,若函数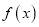 恰有一个零点,求实数
恰有一个零点,求实数 的取值范围;
的取值范围;(2)当
 ,
,  时,对任意
时,对任意 ,有
,有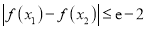 成立,求实数
成立,求实数 的取值范围.
的取值范围.
相关试题

