【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
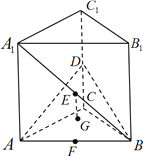
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
参考答案:
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)证线面平行,直接找线线平行即可,构造平行四边形![]() ,证明
,证明![]() 平行于DE,即可得到线线平行,进而得到线面平行。(2)建系,分别求出两个半平面的法向量,根据公式得到法向量的夹角,从而得到二面角的大小。
平行于DE,即可得到线线平行,进而得到线面平行。(2)建系,分别求出两个半平面的法向量,根据公式得到法向量的夹角,从而得到二面角的大小。
(1) 连结 ![]() ,则在三角形
,则在三角形![]() 中
中![]() 为中位线,于是
为中位线,于是![]() ,
, ![]()
因为![]() 为
为![]() 中点,所以
中点,所以![]() 平行且等于
平行且等于![]() . 所以在平行四边形
. 所以在平行四边形![]() 中,
中, ![]() 平行于
平行于![]()
因为![]() 在平面
在平面 ![]() 上,所以
上,所以![]() 平行于平面
平行于平面![]()
(2)分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
设![]() ,则
,则![]()
因为![]() 垂直于平面
垂直于平面![]() ,所以有
,所以有![]() ,
,
解得![]() ,所以
,所以![]()
面![]() 的法向量
的法向量![]() ,面
,面![]() 的法向量为
的法向量为![]()
所以![]()
结合图形知,二面角![]() 的预先为
的预先为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A. 90 B. 75
C. 60 D. 45
-
科目: 来源: 题型:
查看答案和解析>>【题目】读下列各题所给的程序,依据程序画出程序框图,并说明其功能:
(1)INPUT “x=”;x
IF x>1 OR x<-1 THEN
y=1
ELSE y=0
END IF
PRINE y
END
(2)INPUT “输入三个正数a,b,c=”;a,b,c
IF a+b>c AND a+c>b AND b+c>a THEN
p=(a+b+c)/2
S=SQR(p*(p-a)*(p-b)*(p-c))
PRINT “三角形的面积S=”S
ELSE
PRINT “构不成三角形”
END IF
END
-
科目: 来源: 题型:
查看答案和解析>>【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥
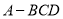 中,
中, 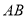 垂直于平面
垂直于平面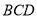 ,
, 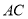 垂直于
垂直于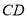 ,且
,且 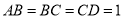 ,则三棱锥
,则三棱锥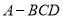 的外接球的球面面积为__________.
的外接球的球面面积为__________.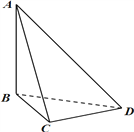
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
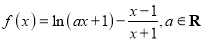 .
.(1)若
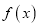 在
在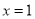 时取到极值,求
时取到极值,求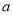 的值及
的值及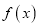 的图象在
的图象在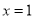 处的切线方程;
处的切线方程;(2)若
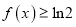 在
在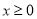 时恒成立,求
时恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以坐标原点
 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线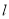 上两点
上两点 的极坐标分别为
的极坐标分别为 ,圆
,圆 的参数方程为
的参数方程为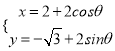 (
( 为参数).
为参数).(1)设
 为线段
为线段 的中点,求直线
的中点,求直线 的平面直角坐标方程;
的平面直角坐标方程;(2)判断直线
 与圆
与圆 的位置关系.
的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知多面体
 的底面
的底面 是边长为
是边长为 的菱形,
的菱形, 
 底面
底面 ,
,  ,且
,且 .
.(1)证明:平面
 平面
平面 ;
;(2)若直线
 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值.
的余弦值.
相关试题

