【题目】已知函数f(x)=loga( ![]() +x)(其中a>1).
+x)(其中a>1).
(1)判断函数y=f(x)的奇偶性,并说明理由;
(2)判断 ![]() (其中m,n∈R,且m+n≠0)的正负,并说明理由.
(其中m,n∈R,且m+n≠0)的正负,并说明理由.
参考答案:
【答案】
(1)解:函数y=f(x)是奇函数,理由如下:
因为 ![]() ,所以函数y=f(x)的定义域为R.
,所以函数y=f(x)的定义域为R.
又因为 ![]() ,
,
所以函数y=f(x)是奇函数
(2)解: ![]() ,理由如下:
,理由如下:
任取0≤x1<x2,设 ![]() ,
,
则 ![]() ,故0<u1<u2,从而
,故0<u1<u2,从而 ![]() .
.
因为a>1,所以 ![]() ,
,
故 ![]() 在[0,+∞)上单调递增.
在[0,+∞)上单调递增.
又因为 ![]() 为奇函数,
为奇函数,
所以f(﹣n)=﹣f(n),且 ![]() 在(﹣∞,+∞)上单调递增.
在(﹣∞,+∞)上单调递增.
所以m+n=m﹣(﹣n)与f(m)+f(n)=f(m)﹣f(﹣n)同号,即 ![]()
【解析】(1)函数y=f(x)是奇函数,理由如下:结合对数的运算性质和函数奇偶性的定义,可证明;(2) ![]() ,结合函数的单调性和奇偶性,可进行判断.
,结合函数的单调性和奇偶性,可进行判断.
【考点精析】利用函数的奇偶性对题目进行判断即可得到答案,需要熟知偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (a>0)在其定义域上为奇函数.
(a>0)在其定义域上为奇函数.
(1)求a的值;
(2)判断函数f(x)的单调性,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=﹣4x2+4ax﹣4a﹣a2在区间[0,1]内有一最大值﹣5,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒)
8
10
12
14
16
每小时生产有缺点的零件数y(件)
5
7
8
9
11
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
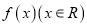 是奇函数,函数
是奇函数,函数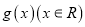 是偶函数,则
是偶函数,则A. 函数
 是奇函数 B. 函数
是奇函数 B. 函数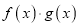 是奇函数
是奇函数C. 函数
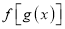 是奇函数 D.
是奇函数 D. 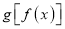 是奇函数
是奇函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天,两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.经统计,两个厂家10天的试销情况茎叶图如下:

(Ⅰ)现从厂家试销的10天中抽取两天,求这两天的销售量都大于40的概率;
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为
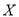 (单位:元),求
(单位:元),求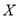 的分布列和数学期望;
的分布列和数学期望;(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场做出选择,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角坐标平面内的两个点P和Q满足条件:①P和Q都在函数y=f(x)的图象上;②P和Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”([P,Q]与[Q,P]看作同一对“友好点对”).已知函数
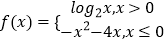 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对
B.1对
C.2对
D.3对
相关试题

