【题目】已知函数f(x)= ![]() (a>0)在其定义域上为奇函数.
(a>0)在其定义域上为奇函数.
(1)求a的值;
(2)判断函数f(x)的单调性,并给出证明.
参考答案:
【答案】
(1)解:由f(﹣x)=﹣f(x)得 ![]() ,解得a=±1.
,解得a=±1.
由因为a>0,所以a=1
(2)解:函数f(x)在R上是增函数,证明如下:
证法一:设x1,x2∈R,且x1<x2,易知 ![]() ,
,
则 ![]() .)
.)
因为x1<x2,所以 ![]() ,
,
所以f(x1)<f(x2),即f(x)是R上的增函数
证法二:∵ ![]() ,
,
∴ ![]() ,
,
∵f′(x)>0恒成立,
∴f(x)是R上的增函数
【解析】(1)由f(﹣x)=﹣f(x)得 ![]() ,解得a的值;(2)函数f(x)在R上是增函数,证法一:设x1 , x2∈R,且x1<x2 , 作差比较f(x1),f(x2)的大小,利用函数单调性的定义,可得f(x)是R上的增函数;
,解得a的值;(2)函数f(x)在R上是增函数,证法一:设x1 , x2∈R,且x1<x2 , 作差比较f(x1),f(x2)的大小,利用函数单调性的定义,可得f(x)是R上的增函数;
证法二:求导,根据′(x)>0恒成立,可得:f(x)是R上的增函数;
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数的奇偶性的理解,了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2﹣3x<0},B={x|(x+2)(4﹣x)≥0},C={x|a<x≤a+1}.
(1)求A∩B;
(2)若B∪C=B,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
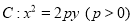 的准线为
的准线为 ,取过焦点
,取过焦点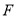 且平行于
且平行于 轴的直线与抛物线交于不同的两点
轴的直线与抛物线交于不同的两点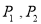 ,过
,过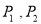 作圆心为
作圆心为 的圆,使抛物线上其余点均在圆外,且
的圆,使抛物线上其余点均在圆外,且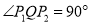 .
. (Ⅰ)求抛物线
 和圆
和圆 的方程;
的方程;(Ⅱ)过点
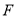 作直线
作直线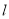 与抛物线
与抛物线 和圆
和圆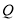 依次交于
依次交于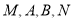 ,求
,求 的最小值.
的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是定义在R上的奇函数,当时x≥0,f(x)=x2+2x.
(1)求函数f(x)的解析式;
(2)解不等式f(x)≥x+2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=﹣4x2+4ax﹣4a﹣a2在区间[0,1]内有一最大值﹣5,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒)
8
10
12
14
16
每小时生产有缺点的零件数y(件)
5
7
8
9
11
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(
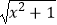 +x)(其中a>1).
+x)(其中a>1).
(1)判断函数y=f(x)的奇偶性,并说明理由;
(2)判断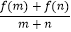 (其中m,n∈R,且m+n≠0)的正负,并说明理由.
(其中m,n∈R,且m+n≠0)的正负,并说明理由.
相关试题

