【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天,两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.经统计,两个厂家10天的试销情况茎叶图如下:

(Ⅰ)现从厂家试销的10天中抽取两天,求这两天的销售量都大于40的概率;
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场做出选择,并说明理由.
参考答案:
【答案】(1) ![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】试题分析:(Ⅰ)利用古典概型求这两天的销售量都大于40的概率;(Ⅱ)(ⅰ)依据题意求离散型随机变量的分布列和数学期望;(ⅱ)利用统计学知识为商场作处选择.
试题解析:
(Ⅰ)记“抽取的两天销售量都大于40”为事件A,
则![]() .
.
(Ⅱ)(ⅰ)设乙产品的日销售量为a,则
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
∴![]() 的所有可能取值为:152,156,160,166,172,
的所有可能取值为:152,156,160,166,172,
∴![]() 的分布列为
的分布列为
| 152 | 156 | 160 | 166 | 172 |
|
|
|
|
|
|
![]() .
.
(ⅱ)依题意,甲厂家的日平均销售量为: ![]() ,
,
∴甲厂家的日平均返利额为: ![]() 元, 由(ⅰ)得乙厂家的日平均返利额为162元(>149元),∴推荐该商场选择乙厂家长期销售.
元, 由(ⅰ)得乙厂家的日平均返利额为162元(>149元),∴推荐该商场选择乙厂家长期销售.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒)
8
10
12
14
16
每小时生产有缺点的零件数y(件)
5
7
8
9
11
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(
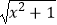 +x)(其中a>1).
+x)(其中a>1).
(1)判断函数y=f(x)的奇偶性,并说明理由;
(2)判断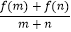 (其中m,n∈R,且m+n≠0)的正负,并说明理由.
(其中m,n∈R,且m+n≠0)的正负,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
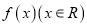 是奇函数,函数
是奇函数,函数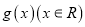 是偶函数,则
是偶函数,则A. 函数
 是奇函数 B. 函数
是奇函数 B. 函数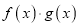 是奇函数
是奇函数C. 函数
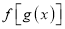 是奇函数 D.
是奇函数 D. 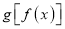 是奇函数
是奇函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】若直角坐标平面内的两个点P和Q满足条件:①P和Q都在函数y=f(x)的图象上;②P和Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”([P,Q]与[Q,P]看作同一对“友好点对”).已知函数
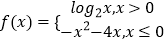 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对
B.1对
C.2对
D.3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
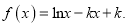
(Ⅰ)若
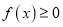 有唯一解,求实数
有唯一解,求实数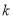 的值;
的值;(Ⅱ)证明:当
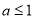 时,
时, 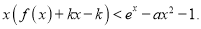
(附:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
P(k2>k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.83
x
2
4
5
6
8
y
30
40
60
50
70
(Ⅰ)画出散点图;
(Ⅱ)求回归直线方程;
(Ⅲ)试预测广告费支出为10万元时,销售额多大?
相关试题

