【题目】已知f(x)=﹣4x2+4ax﹣4a﹣a2在区间[0,1]内有一最大值﹣5,求a的值.
参考答案:
【答案】解:∵f(x)=﹣4x2+4ax﹣4a﹣a2=﹣4(x﹣ ![]() )2﹣4a,对称轴为x=
)2﹣4a,对称轴为x= ![]() ,
,
当a<0时, ![]() <0,∴f(x)在区间[0,1]上是减函数,
<0,∴f(x)在区间[0,1]上是减函数,
它的最大值为f(0)=﹣a2﹣4a=﹣5,
∴a=﹣5,或a=1(不合题意,舍去),
∴a=﹣5;
当a=0时,f(x)=﹣4x2 , 不合题意,舍去;
当0<a<2时,0< ![]() <1,f(x)在区间[0,1]上的最大值是f(
<1,f(x)在区间[0,1]上的最大值是f( ![]() )=﹣4a=﹣5,
)=﹣4a=﹣5,
∴a= ![]() ;
;
当a≥2时, ![]() ≥1,f(x)在区间[0,1]上是增函数,
≥1,f(x)在区间[0,1]上是增函数,
它的最大值为f(1)=﹣4+4a﹣4a﹣a2=﹣5,
∴a=±1,(不合题意,舍去);
综上,a的值是 ![]() 或﹣5
或﹣5
【解析】先求对称轴,比较对称轴和区间的关系,利用二次函数的图象与性质来解答本题.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
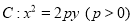 的准线为
的准线为 ,取过焦点
,取过焦点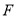 且平行于
且平行于 轴的直线与抛物线交于不同的两点
轴的直线与抛物线交于不同的两点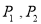 ,过
,过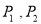 作圆心为
作圆心为 的圆,使抛物线上其余点均在圆外,且
的圆,使抛物线上其余点均在圆外,且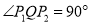 .
. (Ⅰ)求抛物线
 和圆
和圆 的方程;
的方程;(Ⅱ)过点
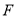 作直线
作直线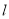 与抛物线
与抛物线 和圆
和圆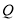 依次交于
依次交于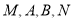 ,求
,求 的最小值.
的最小值.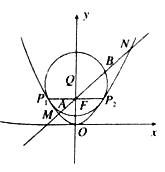
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是定义在R上的奇函数,当时x≥0,f(x)=x2+2x.
(1)求函数f(x)的解析式;
(2)解不等式f(x)≥x+2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (a>0)在其定义域上为奇函数.
(a>0)在其定义域上为奇函数.
(1)求a的值;
(2)判断函数f(x)的单调性,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒)
8
10
12
14
16
每小时生产有缺点的零件数y(件)
5
7
8
9
11
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(
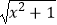 +x)(其中a>1).
+x)(其中a>1).
(1)判断函数y=f(x)的奇偶性,并说明理由;
(2)判断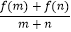 (其中m,n∈R,且m+n≠0)的正负,并说明理由.
(其中m,n∈R,且m+n≠0)的正负,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
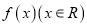 是奇函数,函数
是奇函数,函数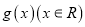 是偶函数,则
是偶函数,则A. 函数
 是奇函数 B. 函数
是奇函数 B. 函数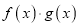 是奇函数
是奇函数C. 函数
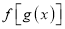 是奇函数 D.
是奇函数 D. 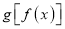 是奇函数
是奇函数
相关试题

