【题目】已知数列{an}满足:a1= ![]() ,a2=
,a2= ![]() ,2an=an+1+an﹣1(n≥2,n∈N),数列{bn}满足:b1<0,3bn﹣bn﹣1=n(n≥2,n∈R),数列{bn}的前n项和为Sn .
,2an=an+1+an﹣1(n≥2,n∈N),数列{bn}满足:b1<0,3bn﹣bn﹣1=n(n≥2,n∈R),数列{bn}的前n项和为Sn .
(1)求证:数列{bn﹣an}为等比数列;
(2)求证:数列{bn}为递增数列;
(3)若当且仅当n=3时,Sn取得最小值,求b1的取值范围.
参考答案:
【答案】
(1)解:∵2an=an+1+an﹣1(n≥2,n∈N),
∴{an}是等差数列.
又∵a1= ![]() ,a2=
,a2= ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,(n≥2,n∈N*),
,(n≥2,n∈N*),
∴bn+1﹣an+1= ![]()
= ![]() =
= ![]()
= ![]() .
.
又∵ ![]() ,
,
∴{bn﹣an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列.
为公比的等比数列.
(2)证明:∵bn﹣an=(b1﹣ ![]() )(
)( ![]() )n﹣1,
)n﹣1, ![]() .
.
∴ ![]() .
.
当n≥2时,bn﹣bn﹣1= ![]() .
.
又b1<0,∴bn﹣bn﹣1>0.
∴{bn}是单调递增数列.
(3)解:∵当且仅当n=3时,Sn取最小值.
∴ ![]() ,即
,即 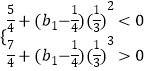 ,
,
∴b1∈(﹣47,﹣11)
【解析】(1)由已知得{an}是等差数列, ![]() ,bn+1﹣an+1=
,bn+1﹣an+1= ![]() =
= ![]() .由此能证明{bn﹣an}是以
.由此能证明{bn﹣an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列.(2)由
为公比的等比数列.(2)由 ![]() .得当n≥2时,bn﹣bn﹣1=
.得当n≥2时,bn﹣bn﹣1= ![]() .由此能证明{bn}是单调递增数列.(3)由已知得
.由此能证明{bn}是单调递增数列.(3)由已知得 ![]() ,由此能求出b1的取值范围.
,由此能求出b1的取值范围.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
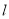 的参数方程为
的参数方程为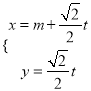 (
(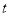 为参数),以坐标原点
为参数),以坐标原点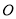 为极点,以
为极点,以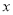 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线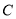 的极坐标方程为
的极坐标方程为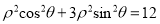 ,且曲线
,且曲线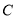 的左焦点
的左焦点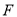 在直线上.
在直线上.(1)若直线
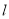 与曲线
与曲线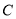 交于
交于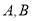 两点,求
两点,求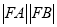 的值;
的值;(2)设曲线
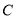 的内接矩形的周长为
的内接矩形的周长为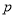 ,求
,求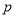 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,
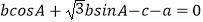 .
.
(1)求角B的大小;
(2)若 ,求a+c的最大值.
,求a+c的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的首项a1=
 ,公比q满足q>0且q≠1,又已知a1 , 5a3 , 9a5成等差数列;
,公比q满足q>0且q≠1,又已知a1 , 5a3 , 9a5成等差数列;
(1)求数列{an}的通项公式;
(2)令bn=log3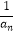 ,记Tn=
,记Tn= 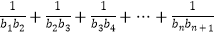 ,是否存在最大的整数m,使得对任意n∈N* , 均有Tn>
,是否存在最大的整数m,使得对任意n∈N* , 均有Tn>  成立?若存在,求出m,若不存在,请说明理由.
成立?若存在,求出m,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an} 中,已知公差
 ,且a1+a3+a5+…+a99=60,则a1+a2+a3+…+a100= .
,且a1+a3+a5+…+a99=60,则a1+a2+a3+…+a100= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A、B两种规格的金属板,每张面积分别为2m2与3m2 . 用A种规格的金属板可造甲种产品3个,乙种产品5个;用B种规格的金属板可造甲、乙两种产品各6个.问A、B两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}、{bn}满足:a1=
 ,an+bn=1,bn+1=
,an+bn=1,bn+1= 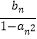 .
.
(1)求a2 , a3;
(2)证数列{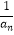 }为等差数列,并求数列{an}和{bn}的通项公式;
}为等差数列,并求数列{an}和{bn}的通项公式;
(3)设Sn=a1a2+a2a3+a3a4+…+anan+1 , 求实数λ为何值时4λSn<bn恒成立.
相关试题

