Question

【题目】如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．
注：年份代码1﹣7分别对应年份2008﹣2014．
（1）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以证明；
（2）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．
附注：
参考数据： =9.32， =40.17， =0.55， ≈2.646．
参考公式： ，
回归方程 中斜率和截距的最小二乘估计公式分别为：
， ．

Answer 1

【答案】
（1）

解：由折线图看出，y与t之间存在较强的正相关关系，理由如下：

∵ = ≈ ≈ ≈0.996，

∵0.996＞0.75，

故y与t之间存在较强的正相关关系；

（2）

解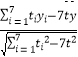： = ≈ ≈0.10，

≈1.331﹣0.10×4≈0.93，

∴y关于t的回归方程 =0.103+0.93，

2016年对应的t值为9，

故 =0.10×9+0.93=1.83，

预测2016年我国生活垃圾无害化处理量为1.83亿吨．

【解析】（1）由折线图看出，y与t之间存在较强的正相关关系，将已知数据代入相关系数方程，可得答案；（2）根据已知中的数据，求出回归系数，可得回归方程，2016年对应的t值为9，代入可预测2016年我国生活垃圾无害化处理量．本题考查的知识点是线性回归方程，回归分析，计算量比较大，计算时要细心．