【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
参考答案:
【答案】A (-1,0),C(5,-6)
【解析】试题分析:由题意, ![]() 点是直线
点是直线![]() 与直线
与直线![]() 的交点,列出方程组即可求出
的交点,列出方程组即可求出![]() 点坐标,由直线
点坐标,由直线![]() 及x轴是∠A的平分线,可求出AC边所在的直线方程,再根据BC边上的高求出BC边所在的直线方程,解出AC边所在的直线方程和BC边所在的直线方程组成的方程组,即可求得
及x轴是∠A的平分线,可求出AC边所在的直线方程,再根据BC边上的高求出BC边所在的直线方程,解出AC边所在的直线方程和BC边所在的直线方程组成的方程组,即可求得![]() 点坐标.
点坐标.
试题解析:由方程组![]() 解得点A的坐标为(-1,0).
解得点A的坐标为(-1,0).
又直线AB的斜率kAB=1,x轴是∠A的平分线,
所以kAC=-1,则AC边所在的直线方程为y=-(x+1).①
又已知BC边上的高所在直线的方程为x-2y+1=0,
故直线BC的斜率kBC=-2,
所以BC边所在的直线方程为y-2=-2(x-1).②
解①②组成的方程组得![]()
即顶点C的坐标为(5,-6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,PA⊥面ABCD,∠DAB=90°,AB平行于CD,AD=CD=2AB=2,E,F分别为PC,CD的中点
(1)求证:AB⊥面BEF;
(2)设PA=h,若二面角E﹣BD﹣C大于45°,求h的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直, 
 为
为 的中点.
的中点.(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 ;
;(3)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若对于任意的x∈[﹣1,0],关于x的不等式3x2+2ax+b≤0恒成立,则a2+b2﹣2的最小值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的有
①刻画一组数据集中趋势的统计量有极差、方差、标准差等;刻画一组数据离散程度统计量有平均数、中位数、众数等.
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大.
③有10个阄,其中一个代表奖品,10个人按顺序依次抓阄来决定奖品的归属,则摸奖的顺序对中奖率没有影响.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若A=
 ,b(1﹣cosC)=ccosA,b=2,则△ABC的面积为( )
,b(1﹣cosC)=ccosA,b=2,则△ABC的面积为( )
A.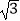
B.2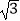
C.
D.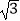 或2
或2 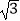

相关试题

