【题目】(本小题满分8分)直线l过点P(4,1),
(1)若直线l过点Q(-1,6),求直线l的方程;
(2)若直线l在y轴上的截距是在x轴上的截距的2倍,求直线l的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
试题分析:(1)由题,此直线经过两点,故采用直线的两点式方程,![]() ,将P(4,1),Q(-1,6),代入到方程中,得到直线方程x+y-5=0;(2)由题,经过一点的直线可设为直线的点斜式,
,将P(4,1),Q(-1,6),代入到方程中,得到直线方程x+y-5=0;(2)由题,经过一点的直线可设为直线的点斜式,![]() ,将点代入,得到y-1=k(x-4),分别将x,y轴上的截距表示出来,由题中的关系可得到k=
,将点代入,得到y-1=k(x-4),分别将x,y轴上的截距表示出来,由题中的关系可得到k=![]() 或k=-2,故直线的方程为y=
或k=-2,故直线的方程为y=![]() x或y=-2x+9.
x或y=-2x+9.
试题解析:解:(1)直线l的方程为![]() =
=![]() ,化简,得x+y-5=0. 4分
,化简,得x+y-5=0. 4分
(2)由题意知直线有斜率,设直线l的方程为y-1=k(x-4),l在y轴上的截距为1-4k,在x轴上的截距为4-![]() ,故1-4k=2(4-
,故1-4k=2(4-![]() ),得k=
),得k=![]() 或k=-2,直线l的方程为y=
或k=-2,直线l的方程为y=![]() x或y=-2x+9. 8分
x或y=-2x+9. 8分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在海岸
 处发现北偏东
处发现北偏东 方向,距
方向,距 处
处 海里的
海里的 处有一艘走私船,在
处有一艘走私船,在 处北偏西
处北偏西 方向,距
方向,距 处
处 海里的
海里的 处的我方辑私船奉命以
处的我方辑私船奉命以 海里/小时的速度追截走私船,此时走私船正以
海里/小时的速度追截走私船,此时走私船正以 海里/小时的速度,以
海里/小时的速度,以 处向北偏东
处向北偏东 方向逃窜.问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①如果
 ,
, 是两条直线,且
是两条直线,且 ,那么
,那么 平行于经过
平行于经过 的任何平面;
的任何平面;②如果直线
 和平面
和平面 满足
满足 ,那么直线
,那么直线 与平面
与平面 内的任何直线平行;
内的任何直线平行;③如果直线
 ,
, 和平面
和平面 满足
满足 ,
, ,那么
,那么 ;
;④如果直线
 ,
, 和平面
和平面 满足
满足 ,
, ,
, ,那么
,那么 ;
;⑤如果平面
 ,
, ,
, 满足
满足 ,
, ,那么
,那么 .
.其中正确命题的序号是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
天气
晴
雨
阴
阴
阴
雨
阴
晴
晴
晴
阴
晴
晴
晴
晴
日期
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
天气
晴
阴
雨
阴
阴
晴
阴
晴
晴
晴
阴
晴
晴
晴
雨
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=1+λan , 其中λ≠0.
(1)证明{an}是等比数列,并求其通项公式;
(2)若S5= ,求λ.
,求λ. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

注:年份代码1﹣7分别对应年份2008﹣2014.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: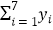 =9.32,
=9.32,  =40.17,
=40.17,  =0.55,
=0.55,  ≈2.646.
≈2.646.
参考公式: ,
,
回归方程 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线l与两直线y=1和x-y-7=0分别交于A,B两点,若线段AB的中点为M(1,-1),则直线l的斜率为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

