【题目】数列{an}的各项均为正数,a1=t,k∈N* , k≥1,p>0,an+an+1+an+2+…+an+k=6pn .
(1)当k=1,p=5时,若数列{an}成等比数列,求t的值;
(2)设数列{an}是一个等比数列,求{an}的公比及t(用p、k的代数式表示);
(3)当k=1,t=1时,设Tn=a1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,参照教材上推导等比数列前n项和公式的推导方法,求证:{
,参照教材上推导等比数列前n项和公式的推导方法,求证:{ ![]() Tn﹣
Tn﹣ ![]() ﹣6n}是一个常数.
﹣6n}是一个常数.
参考答案:
【答案】
(1)解:an+an+1=65n,
an+1+an+2=65n+1,
设等比数列(an}的公比是q,
则an+an+1=65n5,
∴q=5,
n=1时,t+5t=30,∴t=5
(2)解:an+an+1+an+2+…+an+k=6pn,
an+1+an+2+an+3+…+an+1+k=6pn+1,
数列{an}是一个等比数列,所以求出公比为p,
∴t(pn﹣1+pn+…+pn+k﹣1)=6pn,
项数为n+k﹣1﹣(n﹣1)十1=k+1项,
当p=1时,t(k+1)=6,
∴t= ![]() ,
,
当p≠1,且p>0时,t ![]() =6pn,
=6pn,
∴t= ![]()
(3)证明:∵n是任意的正整数,当n=1时, ![]() =6P1=6,
=6P1=6,
依此类推,当n取n﹣1项时, ![]() =
= ![]() =6,
=6,
∴Tn=a1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,
,
![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() =a1+
=a1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,
,
∴(1+ ![]() )Tn=2a1+
)Tn=2a1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() =a1+6n﹣6+
=a1+6n﹣6+ ![]() ,
,
∴ ![]() Tn﹣
Tn﹣ ![]() ﹣6n=a1﹣6=﹣5
﹣6n=a1﹣6=﹣5
【解析】(1)由an+an+1=65n , an+1+an+2=65n+1 , 得到等比数列(an}的公比q=5,由此能求出t的值.(2)an+an+1+an+2+…+an+k=6pn , an+1+an+2+an+3+…+an+1+k=6pn+1 , 数列{an}是一个等比数列,所以求出公比为p,由此能求出t.(3)由Tn=a1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,
, ![]() Tn=a1+
Tn=a1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,由此能够证明
,由此能够证明 ![]() Tn﹣
Tn﹣ ![]() ﹣6n=a1﹣6=﹣5.
﹣6n=a1﹣6=﹣5.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的通项公式的相关知识点,需要掌握通项公式:![]() ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.

注:年份代码1﹣7分别对应年份2008﹣2014.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: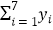 =9.32,
=9.32,  =40.17,
=40.17,  =0.55,
=0.55,  ≈2.646.
≈2.646.
参考公式: ,
,
回归方程 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线l与两直线y=1和x-y-7=0分别交于A,B两点,若线段AB的中点为M(1,-1),则直线l的斜率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又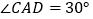 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
(
 )求证:
)求证: .
.(
 )求证:
)求证: 平面
平面 .
.(
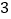 )设平面
)设平面 平面
平面 ,试问:直线
,试问:直线 是否与直线
是否与直线 平行,请说明理由.
平行,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】求满足下列条件的直线的方程:
(1)直线
 经过点
经过点 ,并且它的倾斜角等于直线
,并且它的倾斜角等于直线 的倾斜角的2倍,求直线
的倾斜角的2倍,求直线 的方程;
的方程;(2)直线
 过点
过点 ,并且在
,并且在 轴上的截距是
轴上的截距是 轴上截距的
轴上截距的 ,求直线
,求直线 的方程.
的方程.
相关试题

