【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
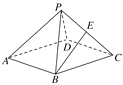
A. BE∥平面PAD,且BE到平面PAD的距离为![]()
B. BE∥平面PAD,且BE到平面PAD的距离为![]()
C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
参考答案:
【答案】D
【解析】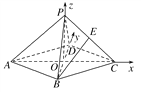
连接AC,BD,交点为O,连接OP,以O为坐标原点,OC,OD,OP所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,由正四棱锥P-ABCD的棱长均为2,点E为PC的中点,知A(-![]() ,0,0),B(0,-
,0,0),B(0,- ![]() ,0),C(
,0),C(![]() ,0,0),D(0,
,0,0),D(0, ![]() ,0),P(0,0,
,0),P(0,0, ![]() ),E
),E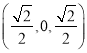 ,则
,则![]() =
= ,
, ![]() =(-
=(-![]() ,0,-
,0,- ![]() ),
), ![]() =(0,
=(0, ![]() ,-
,- ![]() ),设m=(x,y,z)是平面PAD的法向量,则m⊥
),设m=(x,y,z)是平面PAD的法向量,则m⊥![]() ,且m⊥
,且m⊥![]() ,即
,即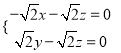 ,令x=1,则z=-1,y=-1,m=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ,则sinθ=
,令x=1,则z=-1,y=-1,m=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ,则sinθ=![]() ,故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°,故选D.
,故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ-2sinθ.
(Ⅰ)求C的参数方程;
(Ⅱ)若点A在圆C上,点B(3,0),求AB中点P到原点O的距离平方的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|3x-1|-2|x|+2.
(Ⅰ)解不等式:f(x)<10;
(Ⅱ)若对任意的实数x,f(x)-|x|≤a恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=
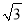 ,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
 AD=1,CD=
AD=1,CD=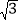 .
.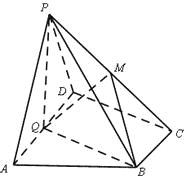
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
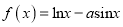 在区间
在区间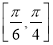 上是单调增函数,则实数
上是单调增函数,则实数 的取值范围为( )
的取值范围为( )A.
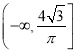 B.
B. 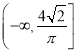 C.
C. 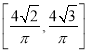 D.
D. 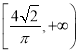
相关试题

