【题目】在直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ-2sinθ.
(Ⅰ)求C的参数方程;
(Ⅱ)若点A在圆C上,点B(3,0),求AB中点P到原点O的距离平方的最大值.
参考答案:
【答案】(Ⅰ) 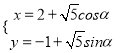 (α为参数)(Ⅱ)
(α为参数)(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ) 已知极坐标方程两边同乘![]() ,利用
,利用![]() ,化简方程得直角坐标方程,从而可求
,化简方程得直角坐标方程,从而可求![]() 的参数方程;(Ⅱ) 利用参数方程,设出中点坐标
的参数方程;(Ⅱ) 利用参数方程,设出中点坐标![]() ,将
,将![]() 中点
中点![]() 到原点
到原点![]() 的距离平方用三角函数表示,根据辅助角公式化简,利用三角函数的有界性,可求
的距离平方用三角函数表示,根据辅助角公式化简,利用三角函数的有界性,可求![]() 中点
中点![]() 到原点
到原点![]() 的距离平方的最大值.
的距离平方的最大值.
试题解析:(Ⅰ)由ρ=4cos θ-2sin θ得ρ2=4ρcos θ-2ρsin θ,
x2+y2=4x-2y,∴(x-2)2+(y+1)2=5,
化为参数方程是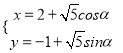 (α为参数).
(α为参数).
(Ⅱ)设点P(x,y),A(x0,y0).
因为点B(3,0),且AB中点为P,
所以![]()
又点A在圆C上,
所以x0=2+![]() cos α,y0=-1+
cos α,y0=-1+![]() sin α,
sin α,
∴x2+y2=![]() +
+![]() =
= +
+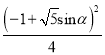 =
=![]() =
=![]() ≤
≤![]() (其中tanφ=5),
(其中tanφ=5),
∴AB中点P到原点O的距离平方的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.

(Ⅰ)求证:平面AB1M⊥平面A1ABB1;
(Ⅱ)过点C作一截面与平面AB1M平行,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
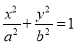 (a>b>0)经过点(
(a>b>0)经过点(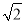 ,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得
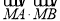 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=a
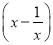 -2ln x(a∈R).
-2ln x(a∈R).(Ⅰ)当a=2时,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若a>
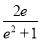 ,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<
,且m,n分别为f(x)的极大值和极小值,S=m-n,求证:S<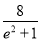 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|3x-1|-2|x|+2.
(Ⅰ)解不等式:f(x)<10;
(Ⅱ)若对任意的实数x,f(x)-|x|≤a恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
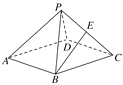
A. BE∥平面PAD,且BE到平面PAD的距离为
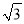
B. BE∥平面PAD,且BE到平面PAD的距离为

C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
相关试题

