【题目】某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
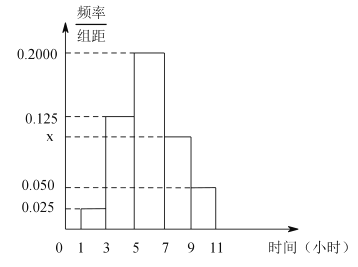
(1)求学习时间在![]() 的学生人数;
的学生人数;
(2)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人学习时间在第四组的概率.
参考答案:
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:(1)由频率分布图求出![]() ,由此能求出学习时间在
,由此能求出学习时间在![]() 的学生人数.
的学生人数.
(2)第三组的学生人数为40人,利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为:第三组的人数为4人,第四组的人数为2人,由此能求出这2人中至少有1人的学习时间在第四组的概率.
试题解析:(1)由频率分布直方图可知: ![]() ,
,
解得![]() ,
,
所以学习时间在![]() 的学生人数为
的学生人数为![]()
(2)第三组的学生人数为![]() ,第三四组共有
,第三四组共有![]() 人,利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为
人,利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为
第三组的人数为为![]() 人,第四组人数为
人,第四组人数为![]() 人
人
设第三组的四位同学为![]() ,第四组的2为同学为
,第四组的2为同学为![]()
则从这六位同学中抽取2位同学有![]()
![]() 共15种可能
共15种可能
其中2人学习时间都不在第四组的有![]() 共6种可能,
共6种可能,
所以这2人中至少有1人的学习时间在第四组的概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(
 )x﹣log2x,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:
)x﹣log2x,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:
①d>a;②d>b;③d<c;④d>c.其中可能成立的是(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
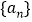 是公差不为零的等差数列,
是公差不为零的等差数列,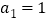 ,且
,且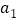 ,
,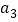 ,
,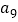 成等比数列.
成等比数列.(1)求数列
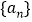 的通项;
的通项;(2)求数列
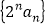 的前
的前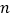 项和
项和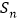 .
. -
科目: 来源: 题型:
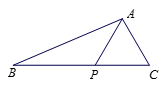
查看答案和解析>>【题目】如图, 在△
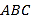 中, 点
中, 点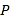 在
在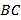 边上,
边上, 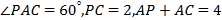 .
.(Ⅰ)求
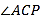 ;
;(Ⅱ)若△
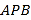 的面积是
的面积是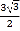 , 求
, 求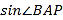 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
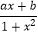 (a,b为常数)是定义在(﹣1,1)上的奇函数,且f(
(a,b为常数)是定义在(﹣1,1)上的奇函数,且f(  )=
)= 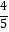
(1)求函数f(x)的解析式;
(2)用定义证明f(x)在(﹣1,1)上是增函数并求值域;
(3)求不等式f(2t﹣1)+f(t)<0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+2ax+2,
(1)求实数a的取值范围,使函数y=f(x)在区间[﹣5,5]上是单调函数;
(2)若x∈[﹣5,5],记y=f(x)的最大值为g(a),求g(a)的表达式并判断其奇偶性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=loga
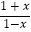 (a>0,且a≠1).
(a>0,且a≠1).
(1)证明f(x)为奇函数;
(2)求使f(x)>0成立的x的集合.
相关试题

