【题目】已知函数f(x)=x2+2ax+2,
(1)求实数a的取值范围,使函数y=f(x)在区间[﹣5,5]上是单调函数;
(2)若x∈[﹣5,5],记y=f(x)的最大值为g(a),求g(a)的表达式并判断其奇偶性.
参考答案:
【答案】
(1)解:∵函数f(x)=x2+2ax+2,
∴对称轴x=﹣a,
根据二次函数的性质得出:当﹣a≤﹣5或﹣a≥5时,f(x)在[﹣5,5]上单调
∴a≥5或a≤﹣5
(2)解:对称轴x=﹣a,
当﹣a≤0,即a≥0,最大值为g(a)=f(5)=27+10a,
当﹣a>0,即a<0,最大值为g(a)=f(﹣5)=27﹣10a,
∴ ![]() ,
,
g(a)=27+|10a|,
∵g(﹣a)=g(a)
∴g(a)为偶函数
【解析】(1)对称轴x=﹣a,当﹣a≤﹣5或﹣a≥5时,f(x)在[﹣5,5]上单调(2)分类得出:当﹣a≤0,即a≥0,最大值为g(a)=f(5)=27+10a,当﹣a>0,即a<0,最大值为g(a)=f(﹣5)=27﹣10a,根据解析式得出奇偶性.
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称,以及对二次函数的性质的理解,了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
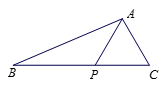
查看答案和解析>>【题目】如图, 在△
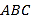 中, 点
中, 点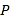 在
在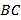 边上,
边上, 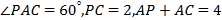 .
.(Ⅰ)求
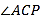 ;
;(Ⅱ)若△
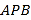 的面积是
的面积是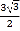 , 求
, 求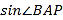 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组
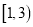 ,第二组
,第二组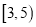 ,第三组
,第三组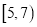 ,第四组
,第四组 ,第五组
,第五组 ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.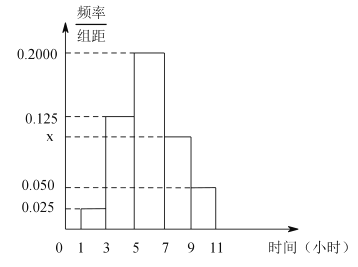
(1)求学习时间在
 的学生人数;
的学生人数;(2)现要从第三组、第四组中用分层抽样的方法抽取6人,从这6人中随机抽取2人交流学习心得,求这2人中至少有1人学习时间在第四组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
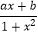 (a,b为常数)是定义在(﹣1,1)上的奇函数,且f(
(a,b为常数)是定义在(﹣1,1)上的奇函数,且f(  )=
)= 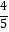
(1)求函数f(x)的解析式;
(2)用定义证明f(x)在(﹣1,1)上是增函数并求值域;
(3)求不等式f(2t﹣1)+f(t)<0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=loga
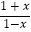 (a>0,且a≠1).
(a>0,且a≠1).
(1)证明f(x)为奇函数;
(2)求使f(x)>0成立的x的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在函数
 (
( )的所有切线中,有且仅有一条切线
)的所有切线中,有且仅有一条切线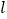 与直线
与直线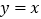 垂直.
垂直.(1)求
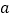 的值和切线
的值和切线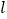 的方程;
的方程;(2)设曲线
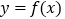 在任一点处的切线倾斜角为
在任一点处的切线倾斜角为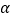 ,求
,求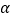 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳
不喜欢游泳
合计
男生
10
女生
20
合计
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为
 .
.(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
 ,其中
,其中 )
)
相关试题

