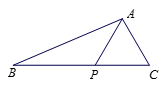
【题目】如图, 在△![]() 中, 点
中, 点![]() 在
在![]() 边上,
边上, ![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)若△![]() 的面积是
的面积是![]() , 求
, 求![]() .
.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(I)根据余弦定理,求得![]() ,则△
,则△![]() 是等边三角形.,故
是等边三角形.,故![]()
(II)由题意可得![]() ,又由
,又由![]() ,可得以
,可得以![]() ,再结合余弦定理可得
,再结合余弦定理可得![]() ,最后由正弦定理可得
,最后由正弦定理可得![]() ,即可得到
,即可得到![]() 的值
的值
试题解析:
(Ⅰ) 在△![]() 中, 因为
中, 因为![]() ,
,
由余弦定理得![]() ,
,
所以![]() ,
,
整理得![]() ,
,
解得![]() .
.
所以![]() .
.
所以△![]() 是等边三角形.
是等边三角形.
所以![]()
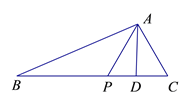
(Ⅱ) 法1: 由于![]() 是△
是△![]() 的外角, 所以
的外角, 所以![]() .
.
因为△![]() 的面积是
的面积是![]() , 所以
, 所以![]() .
.
所以![]() .
.
在△![]() 中,
中, ![]()
![]()
![]() ,
,
所以![]() .
.
在△![]() 中, 由正弦定理得
中, 由正弦定理得![]() ,
,
所以![]() .
.
法2: 作![]() , 垂足为
, 垂足为![]() ,
,
因为△![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,
所以![]() .
.
因为△![]() 的面积是
的面积是![]() , 所以
, 所以![]() .
.
所以![]() . 所以
. 所以![]() .
.
在Rt△![]() 中,
中, ![]() ,
,
所以![]() ,
, ![]() .
.
所以![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
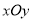 中,直线
中,直线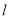 的参数方程是
的参数方程是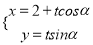 (
(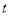 为参数),以
为参数),以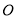 为极点,
为极点, 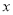 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线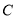 的极坐标方程为
的极坐标方程为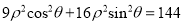 ,且直线
,且直线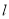 与曲线
与曲线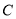 交于
交于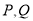 两点.
两点.(Ⅰ)求曲线
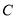 的直角坐标方程及直线
的直角坐标方程及直线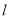 恒过的定点
恒过的定点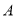 的坐标;
的坐标;(Ⅱ)在(Ⅰ)的条件下,若
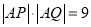 ,求直线
,求直线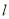 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
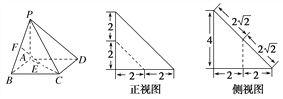
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为
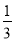 .
.(1)若出现故障的机器台数为
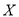 ,求
,求 的分布列;
的分布列;(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
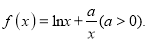
(1)若函数
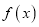 有零点,求实数
有零点,求实数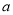 的取值范围;
的取值范围;(2)证明:当
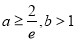 时,
时, 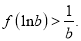
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是
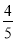 ,乙能答对其中的8道题.规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选;
,乙能答对其中的8道题.规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选;
(Ⅰ)求甲恰有2个题目答对的概率及甲答对题目数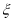 的数学期望与方差。
的数学期望与方差。
(Ⅱ)求乙答对的题目数X的分布列。 -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
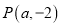 作抛物线
作抛物线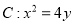 的两条切线, 切点分别为
的两条切线, 切点分别为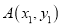 ,
, 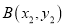 .
.(1) 证明:
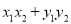 为定值;
为定值;(2) 记△
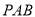 的外接圆的圆心为点
的外接圆的圆心为点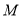 , 点
, 点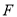 是抛物线
是抛物线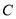 的焦点, 对任意实数
的焦点, 对任意实数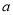 , 试判断以
, 试判断以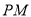 为直径的圆是否恒过点
为直径的圆是否恒过点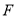 ? 并说明理由.
? 并说明理由.
相关试题

