【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在,且
;(2)存在,且![]() .
.
【解析】试题分析:(1)设出圆心![]() 坐标,根据直线
坐标,根据直线![]() 与圆
与圆![]() 相切,得到圆心到直线
相切,得到圆心到直线![]() 的距离
的距离![]() ,确定出圆心
,确定出圆心![]() 坐标,即可得出圆
坐标,即可得出圆![]() 方程;(2)当直线
方程;(2)当直线![]() 轴,则
轴,则![]() 轴平分
轴平分![]() ,当直线
,当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 方程为
方程为![]() ,联立圆与直线方程,消去
,联立圆与直线方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若
的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若![]() 轴平分
轴平分![]() ,则
,则![]() ,求出
,求出![]() 的值,确定出此时
的值,确定出此时![]() 坐标即可.
坐标即可.
试题解析:(1)设圆心C(a,0) ![]() ,则
,则![]() 或a=-5(舍),所以圆C:x2+y2=4.
或a=-5(舍),所以圆C:x2+y2=4.
(2)当直线AB⊥x轴时,x轴平分∠ANB,当直线AB的斜率存在时,设直线AB的方程为y=k(x-1),N(t,0),A(x1,y1),B(x2,y2),由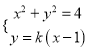 得(k2+1)x2-2k2x+k2-4=0,所以
得(k2+1)x2-2k2x+k2-4=0,所以![]() ,
, ![]() ,若x轴平分∠ANB,则
,若x轴平分∠ANB,则![]()
![]() 2x1x2-(t+1)(x1+x2)+2t=0
2x1x2-(t+1)(x1+x2)+2t=0![]() ,所以当点N为(4,0)时,能使得∠ANM=∠BNM总成立.
,所以当点N为(4,0)时,能使得∠ANM=∠BNM总成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC.

(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,曲线y=x2-6x+1与
 轴交于
轴交于 点,与
点,与 轴交于
轴交于 ,
,  两点.
两点.(1)求△
 的面积;
的面积;(2)求△
 外接圆的方程.
外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=1+mi(i是虚数单位,m∈R),且
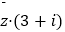 为纯虚数(
为纯虚数(  是z的共轭复数).
是z的共轭复数).
(1)设复数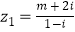 ,求|z1|;
,求|z1|;
(2)设复数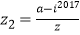 ,且复数z2所对应的点在第四象限,求实数a的取值范围.
,且复数z2所对应的点在第四象限,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】锐角三角形
 中,
中,  ,
,  ,则
,则 面积的取值范围为( )
面积的取值范围为( )A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
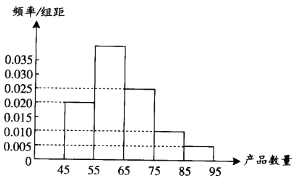
查看答案和解析>>【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点O和点F2(﹣
 ,0)分别为双曲线
,0)分别为双曲线  =1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则
=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则  的取值范围为 .
的取值范围为 .
相关试题

