搜索
【题目】锐角三角形
中， 
， 
，则
面积的取值范围为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】B
【解析】∵∠A=30°，BC=1，可得： 
∴AB=2sinC，AC=2sinB=2sin（150°-C）=2（
cosC+
sinC）=cosC+
sinC，∴S△ABC=
∵C∈（
， 
），可得：2C-
∈（0， 
），∴sin（2C-
）∈（0，1]，可得：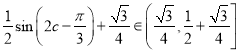 
则△ABC面积的取值范围为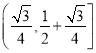
故选B.
点睛: 解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题通法思路是：全部转化为角的关系，建立函数关系式，如
，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，曲线y＝x2－6x＋1与
轴交于
点，与
轴交于
， 
两点．(1)求△
的面积；(2)求△
外接圆的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知复数z＝1＋mi（i是虚数单位，m∈R），且
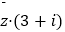为纯虚数（ 
是z的共轭复数）．
（1）设复数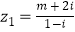
，求|z1|；
（2）设复数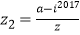
，且复数z2所对应的点在第四象限，求实数a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l：4x＋3y＋10＝0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方．
(1)求圆C的方程；
(2)过点M(1，0)的直线与圆C交于A，B两点(A在x轴上方)，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量．产品数量的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95）由此得到频率分布直方图如图．则产品数量位于[55，65）范围内的频率为；这20名工人中一天生产该产品数量在[55，75）的人数是 ．
-
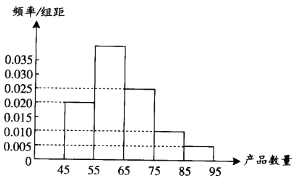
科目： 来源： 题型：
查看答案和解析>>【题目】若点O和点F2（﹣
，0）分别为双曲线 
=1（a＞0）的中心和左焦点，点P为双曲线右支上的任意一点，则 
的取值范围为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，A、B、C的对边分别为a、b、c，且
成等差数列.（Ⅰ）求B的值；
（Ⅱ）求
的范围
相关试题
