【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
参考答案:
【答案】
(1)证明:∵PM是圆O的切线,NAB是圆O的割线,N是PM的中点,
∴MN2=PN2=NANB,
∴ ![]() =
= ![]() ,
,
又∵∠PNA=∠BNP,
∴△PNA∽△BNP,
∴∠APN=∠PBN,即∠APM=∠PBA,.
∵MC=BC,
∴∠MAC=∠BAC,
∴∠MAP=∠PAB,
∴△APM∽△ABP
(2)证明:∵∠ACD=∠PBN,
∴∠ACD=∠PBN=∠APN,即∠PCD=∠CPM,
∴PM∥CD.
∵△APM∽△ABP,
∴∠PMA=∠BPA
∵PM是圆O的切线,
∴∠PMA=∠MCP,
∴∠PMA=∠BPA=∠MCP,即∠MCP=∠DPC,
∴MC∥PD,
∴四边形PMCD是平行四边形
【解析】(1)由切割线定理,及N是PM的中点,可得PN2=NANB,进而 ![]() =
= ![]() ,结合∠PNA=∠BNP,可得△PNA∽△BNP,则∠APN=∠PBN,即∠APM=∠PBA;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP(2)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.
,结合∠PNA=∠BNP,可得△PNA∽△BNP,则∠APN=∠PBN,即∠APM=∠PBA;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP(2)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x-3)2+(y-4)2=1,设点P是圆C上的动点.记d=|PB|2+|PA|2,其中A(0,1),B(0,-1),则d的取值范围为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
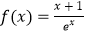 ,
, 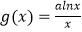 ,(a>0).若对任意实数x1 , 都存在正数x2 , 使得g(x2)=f(x1)成立,则实数a的取值范围是 .
,(a>0).若对任意实数x1 , 都存在正数x2 , 使得g(x2)=f(x1)成立,则实数a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知A(5,-2),B(7,3),且AC边的中点M在y轴上,BC的中点N在x轴上.

(1)求点C的坐标;
(2)求
 边上的中线所在直线方程.
边上的中线所在直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,曲线y=x2-6x+1与
 轴交于
轴交于 点,与
点,与 轴交于
轴交于 ,
,  两点.
两点.(1)求△
 的面积;
的面积;(2)求△
 外接圆的方程.
外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=1+mi(i是虚数单位,m∈R),且
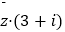 为纯虚数(
为纯虚数(  是z的共轭复数).
是z的共轭复数).
(1)设复数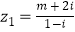 ,求|z1|;
,求|z1|;
(2)设复数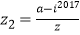 ,且复数z2所对应的点在第四象限,求实数a的取值范围.
,且复数z2所对应的点在第四象限,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
相关试题

