Question

【题目】在平面直角坐标系xOy中，直线l的参数方程为 （ t为参数）．以原点为极点，x轴正半轴为极轴 建立极坐标系，圆C的方程为 ρ=2 sinθ．
（1）写出直线l的普通方程和圆C的直角坐标方程；
（2）若点P的直角坐标为（1，0），圆C与直线l交于A，B两点，求|PA|+|PB|的值．

Answer 1

【答案】
（1）解：直线l的参数方程为 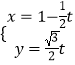（ t为参数）．

消去参数得直线普通方程为 x+y﹣ =0，

由圆C的方程为 ρ=2 sinθ，即ρ2=2 ρsinθ，

可得圆C的直角坐标方程：x2+y2=2 y．

（2）解：直线l的参数方程为 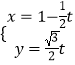（ t为参数）．

把直线l的参数方程代入圆C的直角坐标方程，得t2﹣4t+1=0，△＞0．

∴t1+t2=4，t1t2=1．

∴|PA|+|PB|=|t1|+|t2|=|t1+t2|=4．

【解析】（1）直线l的参数方程为 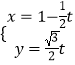（ t为参数）．消去参数得直线普通方程，由圆C的方程为 ρ=2 sinθ，即ρ2=2 ρsinθ，利用互化公式可得圆C的直角坐标方程．（2）把直线l的参数方程代入圆C的直角坐标方程，得t2﹣4t+1=0，△＞0．利用|PA|+|PB|=|t1|+|t2|=|t1+t2|．即可得出．
【考点精析】根据题目的已知条件，利用直线的参数方程的相关知识可以得到问题的答案，需要掌握经过点，倾斜角为的直线的参数方程可表示为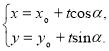（为参数）．