【题目】下列函数中,在区间(0,+∞)上单调递增的是( )
A.y= ![]()
B.y=1﹣x
C.y=x2﹣x
D.y=1﹣x2
参考答案:
【答案】A
【解析】解:函数y= ![]() 的导函数y′=
的导函数y′= ![]() ,在区间(0,+∞)上,y′>0恒成立,故函数在区间(0,+∞)上单调递增;
,在区间(0,+∞)上,y′>0恒成立,故函数在区间(0,+∞)上单调递增;
函数y=1﹣x的导函数y′=﹣1,在区间(0,+∞)上,y′<0恒成立,故函数在区间(0,+∞)上单调递减;
函数y=x2﹣x的导函数y′=2x﹣1,在区间(0, ![]() )上,y′<0恒成立,故函数在区间(0,+∞)上不单调递增;
)上,y′<0恒成立,故函数在区间(0,+∞)上不单调递增;
函数y=1﹣x2的导函数y′=﹣2x,在区间(0,+∞)上,y′<0恒成立,故函数在区间(0,+∞)上单调递减;
故选A.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形
 中,
中,  ,
,  ,平面
,平面 平面
平面 ,
,  为等边三角形,
为等边三角形,  分别是
分别是 的中点,
的中点,  .
.(1)证明:

 ;
;(2)证明:
 平面
平面 ;
;(3)若
 ,求几何体
,求几何体 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列函数:①f(x)=
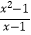 ,g(x)=x+1;②f(x)=|x|,g(x)=
,g(x)=x+1;②f(x)=|x|,g(x)= 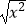 ;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函数的是( )
;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函数的是( )
A.①②③
B.①③
C.②③
D.② -
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇兑起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是 ;
(2)请你估计袋中红球接近 个. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
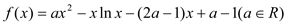 .
.(1)当
 时,求函数
时,求函数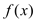 在点
在点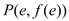 处的切线方程;
处的切线方程;(2)对任意的
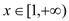 函数
函数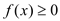 恒成立,求实数
恒成立,求实数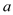 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)设抛物线的顶点在坐标原点,焦点
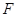 在
在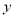 轴正半轴上,过点
轴正半轴上,过点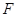 的直线交抛物线于
的直线交抛物线于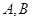 两点,线段
两点,线段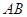 的长是
的长是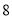 ,
,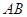 的中点到
的中点到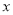 轴的距离是
轴的距离是 .
.(1)求抛物线的标准方程;
(2)在抛物线上是否存在不与原点重合的点
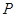 ,使得过点
,使得过点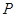 的直线交抛物线于另一点
的直线交抛物线于另一点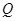 ,满足
,满足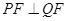 ,且直线
,且直线 与抛物线在点
与抛物线在点 处的切线垂直?并请说明理由.
处的切线垂直?并请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
 中,棱长为1 ,点
中,棱长为1 ,点 为线段
为线段 上的动点(包含线段端点),则下列结论正确的______.
上的动点(包含线段端点),则下列结论正确的______.①当
 时,
时,  平面
平面 ;
;②当
 时,
时,  平面
平面 ;
;③
 的最大值为
的最大值为 ;
; ④
 的最小值为
的最小值为 .
.
相关试题

