【题目】如图,直角梯形![]() 中,
中, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() 分别是
分别是![]() 的中点,
的中点, ![]() .
.
(1)证明: ![]()
![]() ;
;
(2)证明: ![]() 平面
平面![]() ;
;
(3)若![]() ,求几何体
,求几何体![]() 的体积.
的体积.

参考答案:
【答案】(1)由![]() 为等边三角形,
为等边三角形, ![]() 是
是![]() 的中点知
的中点知![]() ,由平面
,由平面![]() 平面
平面![]() 及面面垂直性质定理知,
及面面垂直性质定理知, ![]() 平面
平面![]() ,再由线面垂直定义得EF⊥CD;(2)取AE的中点G,连结MG,DG,因为M是BE的中点,所以MG∥且等于AB的一半,又因为AB∥CD且AB=
,再由线面垂直定义得EF⊥CD;(2)取AE的中点G,连结MG,DG,因为M是BE的中点,所以MG∥且等于AB的一半,又因为AB∥CD且AB= ![]() ,
, ![]() ,所以DN平行且等于MG,所以MGDN是平行四边形,所以MN∥DG,由线面平行的判定定理可得MN∥面ADE;(3)由(1)知EF⊥面ABCD,所以EF是四棱锥E-ABCD的高,由△BEC为正三角形,BC=2,可求得EF的长,由题知ABCD为直角梯形,AB⊥BC,AB=1,BC=2,所以DC=2AB=2,可求出底面ABCD的面积,所以四棱锥D-ABCD的体积就等于
,所以DN平行且等于MG,所以MGDN是平行四边形,所以MN∥DG,由线面平行的判定定理可得MN∥面ADE;(3)由(1)知EF⊥面ABCD,所以EF是四棱锥E-ABCD的高,由△BEC为正三角形,BC=2,可求得EF的长,由题知ABCD为直角梯形,AB⊥BC,AB=1,BC=2,所以DC=2AB=2,可求出底面ABCD的面积,所以四棱锥D-ABCD的体积就等于![]() .
.
【解析】试题分析:(1)(2)(3)
试题解析:(1)证明: ![]()
![]() 为等边三角形,
为等边三角形, ![]() 是
是![]() 的中点
的中点
![]()
![]() 1分
1分
又因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
, ![]() 平面
平面![]()
根据面面垂直的性质定理得![]() 平面
平面![]() ; 3分
; 3分
又![]()
![]() 平面
平面![]()
![]()
![]()
![]() 4分
4分
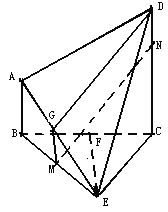
(2)证明:取![]() 中点G,连接
中点G,连接![]()
![]()
![]()
![]()
![]() ,且
,且![]() 6分
6分
![]()
![]() ,
, ![]()
![]()
![]() ,且
,且![]() 8分
8分
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]() 9分
9分
又![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
![]()
![]() 平面
平面![]() 10分
10分
(3)解:依题,直角梯形![]() 中,
中, ![]()
则直角梯形![]() 的面积为
的面积为![]() 12分
12分
由(1)可知![]() 平面
平面![]() ,
, ![]() 是四棱锥
是四棱锥![]() 的高
的高
在等边![]() 中,由边长
中,由边长![]() ,得
,得![]() 13分
13分
故几何体![]() 的体积为
的体积为
![]() 14分
14分
考点: 线面垂直定义;面面垂直性质定理;线面平行的判定;简单几何体体积计算;逻辑推理能力;运算求解能力
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体
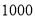 名学生中随机抽取了
名学生中随机抽取了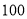 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.年级名次
是否近视
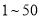

近视
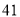
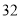
不近视
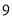
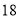
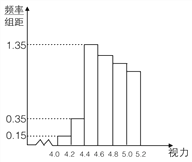
(1)若直方图中后四组的频数成等差数列,试估计全 年级视力在
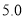 以下的人数;
以下的人数;(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在
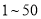 名和
名和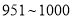 名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过
名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过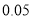 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系? 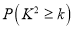
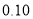
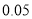

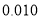
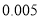
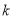


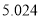
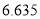
7.879

附:

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=﹣x2+(3﹣2m)x+2+m(0<m≤1).
(1)若x∈[0,m],证明:f(x)≤ ;
;
(2)求|f(x)|在[﹣1,1]上的最大值g(m). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
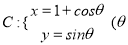 为参数
为参数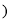 和直线
和直线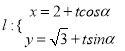
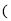 其中
其中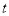 为参数,
为参数, 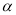 为直线
为直线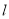 的倾斜角
的倾斜角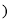 .
.(1)当
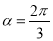 时,求圆上的点到直线
时,求圆上的点到直线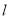 的距离的最小值;
的距离的最小值;(2)当直线
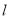 与圆
与圆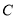 有公共点时,求
有公共点时,求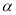 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列函数:①f(x)=
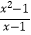 ,g(x)=x+1;②f(x)=|x|,g(x)=
,g(x)=x+1;②f(x)=|x|,g(x)= 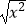 ;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函数的是( )
;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函数的是( )
A.①②③
B.①③
C.②③
D.② -
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇兑起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是 ;
(2)请你估计袋中红球接近 个. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,在区间(0,+∞)上单调递增的是( )
A.y=
B.y=1﹣x
C.y=x2﹣x
D.y=1﹣x2
相关试题

