【题目】(本小题满分12分)设抛物线的顶点在坐标原点,焦点![]() 在
在![]() 轴正半轴上,过点
轴正半轴上,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,线段
两点,线段![]() 的长是
的长是![]() ,
,![]() 的中点到
的中点到![]() 轴的距离是
轴的距离是![]() .
.
(1)求抛物线的标准方程;
(2)在抛物线上是否存在不与原点重合的点![]() ,使得过点
,使得过点![]() 的直线交抛物线于另一点
的直线交抛物线于另一点![]() ,满足
,满足![]() ,且直线
,且直线![]() 与抛物线在点
与抛物线在点![]() 处的切线垂直?并请说明理由.
处的切线垂直?并请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() .
.
【解析】试题分析:(1)求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置,开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数![]() ,只需一个条件就可以确定抛物线的标准方程;(2)在解决与抛物线性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此;(3)解决直线和抛物线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与抛物线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
,只需一个条件就可以确定抛物线的标准方程;(2)在解决与抛物线性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此;(3)解决直线和抛物线的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与抛物线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式![]() :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:(1)设抛物线的方程是![]() ,
,![]() ,
,
由抛物线定义可知![]() 2分
2分
又![]() 中点到
中点到![]() 轴的距离为3,∴
轴的距离为3,∴![]()
![]() ,∴p=2,
,∴p=2,
所以抛物线的标准方程是![]() . 4分
. 4分
(2)设![]() ,则
,则![]() 在
在![]() 处的切线方程是
处的切线方程是![]() ,
,
直线![]() 代入
代入![]() 得
得![]() , 6分
, 6分
故![]() ,所以
,所以![]() 8分
8分
而![]()
![]()
![]() 10分
10分
![]()
![]() ,得
,得![]() ,所以
,所以![]() ,
,
存在点![]() . 12分
. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇兑起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是 ;
(2)请你估计袋中红球接近 个. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,在区间(0,+∞)上单调递增的是( )
A.y=
B.y=1﹣x
C.y=x2﹣x
D.y=1﹣x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
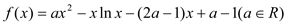 .
.(1)当
 时,求函数
时,求函数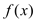 在点
在点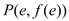 处的切线方程;
处的切线方程;(2)对任意的
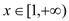 函数
函数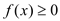 恒成立,求实数
恒成立,求实数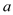 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
 中,棱长为1 ,点
中,棱长为1 ,点 为线段
为线段 上的动点(包含线段端点),则下列结论正确的______.
上的动点(包含线段端点),则下列结论正确的______.①当
 时,
时,  平面
平面 ;
;②当
 时,
时,  平面
平面 ;
;③
 的最大值为
的最大值为 ;
; ④
 的最小值为
的最小值为 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时掷两个骰子,
(1)指出点数的和是3的倍数的各种情形,并判断是否为互斥事件;
(2)求点数的和是3的倍数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在2014年上半年的收入x(单位:万元)与月支出y(单位:万元)的统计资料如下表所示:
月份
1月份
2月份
3月份
4月份
5月份
6月份
收入x
12.3
14.5
15.0
17.0
19.8
20.6
支出Y
5.63
5.75
5.82
5.89
6.11
6.18
根据统计资料,则( )
A.月收入的中位数是15,x与y有正线性相关关系
B.月收入的中位数是17,x与y有负线性相关关系
C.月收入的中位数是16,x与y有正线性相关关系
D.月收入的中位数是16,x与y有负线性相关关系
相关试题

