【题目】已知全集U={R},集合A={x|log2(3﹣x)≤2},集合B= ![]() .
.
(1)求A,B;
(2)求(CUA)∩B.
参考答案:
【答案】
(1)解:由已知得:log2(3﹣x)≤log24,∴ ![]()
解得﹣1≤x<3,∴A={x|﹣1≤x<3}.
![]() =x|﹣2<x≤3
=x|﹣2<x≤3
∴B={x|﹣2<x≤3}
(2)解:由(I)可得CUA={x|x<﹣1或x≥3}.
故(CUA)∩B={x|﹣2<x<﹣1或x=3}
【解析】(1)通过解对数不等式化简集合A,通过解分式不等式化简集合B.(2)利用补集的定义求出集合A的补集;再利用交集的定义求出集合的交集.
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四名同学根据各自的样本数据研究变量
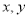 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:( )①
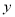 与
与 负相关且
负相关且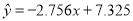 . ②
. ②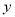 与
与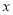 负相关且
负相关且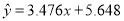
③
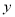 与
与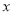 正相关且
正相关且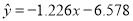 ④
④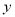 与
与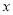 正相关且
正相关且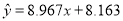
其中正确的结论的序号是( )
A. ①② B. ②③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
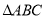 中,
中, 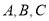 成等差数列是
成等差数列是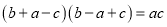 的( )
的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点
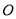 ,焦点在
,焦点在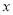 轴上的椭圆
轴上的椭圆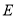 过点
过点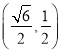 ,离心率为
,离心率为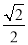 .
.(1)求椭圆
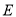 的方程;
的方程;(2)直线
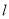 过椭圆
过椭圆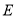 的左焦点
的左焦点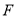 ,且与椭圆
,且与椭圆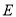 交于
交于 两点,若
两点,若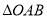 的面积为
的面积为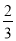 ,求直线
,求直线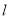 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一系列函数的解析式和值域相同,但是定义域不同,则称这些函数为“同族函数”,例如函数y=x2 , x∈[1,2],与函数y=x2 , x∈[﹣2,﹣1]即为“同族函数”.下面的函数解析式也能够被用来构造“同族函数”的是( )
A.y=x
B.y=|x﹣3|
C.y=2x
D.y=log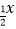
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入
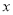 (十万元)与利润
(十万元)与利润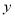 (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据: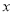
2
3
4
5
6
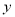
2
4
5
6
7
若由资料知
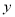 对
对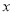 呈线性相关关系。试求:
呈线性相关关系。试求:(1)线性回归方程
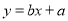 ;
; (2)估计
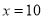 时,利润是多少?
时,利润是多少?附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
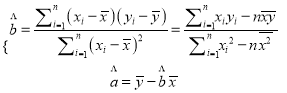
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为
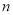 )进行统计.按照
)进行统计.按照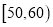 ,
, 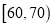 ,
, 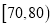 ,
, 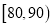 ,
, 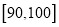 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在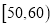 ,
, 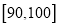 的数据).
的数据).
(1)求样本容量
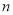 和频率分布直方图中的
和频率分布直方图中的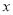 、
、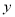 的值;
的值;(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国汉字听写大会”,求所抽取的2名学生中至少有一人得分在
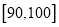 内的概率.
内的概率.
相关试题

