【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若![]() ,求
,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
参考答案:
【答案】见解析
【解析】(Ⅰ)由椭圆的离心率![]() ,可得
,可得![]() .
.
所以![]() ,所以
,所以![]() .
.
又因为点![]() 在椭圆上,
在椭圆上,
所以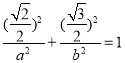 ,即
,即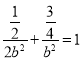 ,解得
,解得![]() ,故
,故![]() .
.
∴椭圆![]() 的方程为
的方程为![]() . -----------------4分
. -----------------4分
(Ⅱ)椭圆的左焦点为![]() .
.
(ⅰ)当![]() 时,
时,![]() .
.
故直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由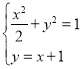 ,消元得
,消元得![]() ,解得
,解得![]() 或
或![]() .
.
由题意可得![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
由/span>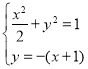 ,消元得
,消元得![]() ,解得
,解得![]() 或
或![]() .
.
由题意可得![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
所以点![]() 到直线
到直线![]() 的距离
的距离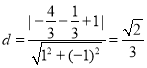 .
.
而![]() ,所以
,所以![]() 的面积
的面积![]() .--------------- 8分
.--------------- 8分
(ⅱ)设直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() .
.
联立方程组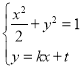 ,消去
,消去![]() ,得
,得![]() ,-------------10分
,-------------10分
由根与系数的关系可得![]() ,
,![]() .
.
所以![]()
![]()
![]() ,
,
所以![]() ,即
,即![]() ,
,
代入整理,![]() ,即
,即![]() . -----------------13分
. -----------------13分
所以直线![]() 的方程为
的方程为![]() ,所以直线
,所以直线![]() 总过定点
总过定点![]() . -----------------14分
. -----------------14分
【命题意图】本题考查椭圆的方程与性质、直线和椭圆的位置关系、三角形面积的求解以及定点的探究性问题,意在考查基本的逻辑推理能力、运算能力和数学应用意识等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
已知直线l经过点
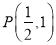 ,倾斜角
,倾斜角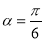 ,圆
,圆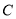 的极坐标方程为
的极坐标方程为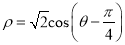 .
.(Ⅰ)写出直线l的参数方程,并把圆
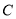 的方程化为直角坐标方程;
的方程化为直角坐标方程;(Ⅱ)设l与圆
 相交于
相交于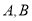 两点,求点
两点,求点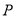 到
到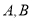 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别
男
女
总计
中年组
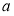
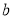
91
老年组
16
已知中年组女性选手人数是仅比老年组女性选手人数多2人.若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(Ⅰ)求表格中的数据
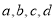 ;
;(Ⅱ)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I) 讨论函数
 的单调区间;
的单调区间;(II)当
 时,若函数
时,若函数 在区间
在区间 上的最大值为3,求
上的最大值为3,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
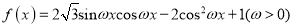 ,且
,且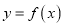 的图象与直线
的图象与直线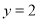 的两个相邻公共点之间的距离为
的两个相邻公共点之间的距离为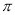 .
.(1)求函数
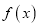 的解析式,并求出
的解析式,并求出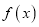 的单调递增区间;
的单调递增区间;(2)将函数
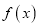 的图象上所有点向左平移
的图象上所有点向左平移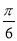 个单位,得到函数
个单位,得到函数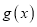 的图象,设
的图象,设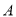 ,
, 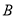 ,
, 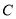 为
为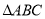 的三个内角,若
的三个内角,若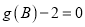 ,且向量
,且向量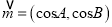 ,
, 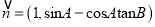 ,求
,求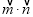 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间
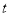 (单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.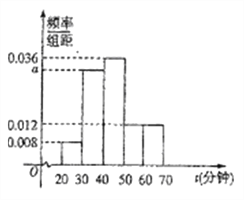
(1)求
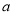 的值;
的值;(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为
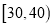 ,
, 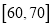 的两组中各抽取多少人?
的两组中各抽取多少人?
相关试题

