【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
参考答案:
【答案】
(1)解:要使函数有意义:则有 ![]() ,解得﹣3<x<1,
,解得﹣3<x<1,
所以函数f(x)的定义域为(﹣3,1)
(2)解:f(x)=loga(1﹣x)+loga(x+3)=loga(1﹣x)(x+3)= ![]() =
= ![]() ,
,
∵﹣3<x<1,∴0<﹣(x+1)2+4≤4,
∵0<a<1,∴ ![]() ≥loga4,即f(x)min=loga4;
≥loga4,即f(x)min=loga4;
由loga4=﹣4,得a﹣4=4,
∴a= ![]() =
= ![]()
【解析】(1)只要使1﹣x>0,x+3>0同时成立即可;(2)先把f(x)化为f(x)= ![]() ,再由二次函数性质及对数函数的单调性可求出f(x)的最小值,根据最小值为﹣4,列方程解出即可.
,再由二次函数性质及对数函数的单调性可求出f(x)的最小值,根据最小值为﹣4,列方程解出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
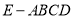 中,底面
中,底面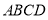 为平行四边形,其中
为平行四边形,其中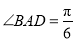 ,
,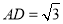 ,
,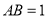 ,等边
,等边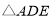 所在平面与平面
所在平面与平面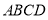 垂直.
垂直.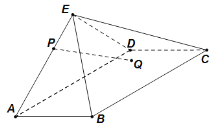
(Ⅰ)点
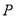 在棱
在棱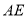 上,且
上,且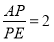 ,
,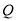 为
为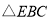 的重心,求证:
的重心,求证: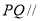 平面
平面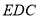 ;
;(Ⅱ)求三棱锥
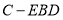 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义在R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0<x<1},则A中所有元素之和为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
已知直线l经过点
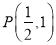 ,倾斜角
,倾斜角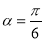 ,圆
,圆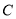 的极坐标方程为
的极坐标方程为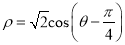 .
.(Ⅰ)写出直线l的参数方程,并把圆
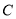 的方程化为直角坐标方程;
的方程化为直角坐标方程;(Ⅱ)设l与圆
 相交于
相交于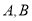 两点,求点
两点,求点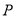 到
到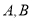 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别
男
女
总计
中年组
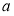
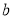
91
老年组
16
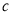
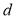
已知中年组女性选手人数是仅比老年组女性选手人数多2人.若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(Ⅰ)求表格中的数据
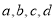 ;
;(Ⅱ)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
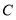 :
: 的离心率为
的离心率为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆
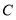 的方程;
的方程;(Ⅱ)已知椭圆的左焦点为
 ,直线
,直线 与椭圆
与椭圆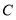 交于不同两点
交于不同两点 ,
, (
( 都在
都在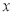 轴上方),且
轴上方),且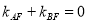 .
.(ⅰ)若
 ,求
,求 的面积;
的面积;(ⅱ)直线
 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I) 讨论函数
 的单调区间;
的单调区间;(II)当
 时,若函数
时,若函数 在区间
在区间 上的最大值为3,求
上的最大值为3,求 的取值范围.
的取值范围.
相关试题

