【题目】现有![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:

设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn.
(1)求p2的值;
(2)证明:pn>![]() .
.
参考答案:
【答案】(1)![]() .(2)见解析.
.(2)见解析.
【解析】试题分析:(1)由题意得![]() ,即可求解
,即可求解![]() 的值;
的值;
(2)根据排列组合的知识得到![]() ,在利用
,在利用![]() 展开式,即可作出证明。
展开式,即可作出证明。
试题解析:
(1)由题意知p2=![]() =, 即p2的值为.
=, 即p2的值为.
(2)先排第n行,则最大数在第n行的概率为![]() =
=![]() ;
;
去掉第n行已经排好的n个数,
则余下的![]() -n=
-n=![]() 个数中最大数在第n-1行的概率为
个数中最大数在第n-1行的概率为![]() =;
=;
故pn=![]() ××…×=
××…×=![]() =
=![]() .
.
由于2n=(1+1)n=C+C+C+…+C≥C+C+C>C+C=C,
故![]() >
>![]() ,即pn>
,即pn>![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,数列{bn},{cn}满足 (n+1) bn=an+1
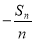 ,(n+2) cn=
,(n+2) cn=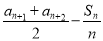 ,其中n∈N*.
,其中n∈N*.(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切n∈N*,有bn≤λ≤cn,求证:数列{an}是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
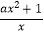 ,且f(1)=﹣1.
,且f(1)=﹣1.
(1)求f(x)的解析式,并判断它的奇偶性;
(2)判断函数f(x)在(0,+∞)上的单调性并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log4(2x+3﹣x2).
(1)求f(x)的定义域及单调区间;
(2)求f(x)的最大值,并求出取得最大值时x的值;
(3)设函数g(x)=log4[(a+2)x+4],若不等式f(x)≤g(x)在x∈(0,3)上恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:全集U=R,函数
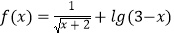 的定义域为集合A,集合B={x|x2﹣a<0}
的定义域为集合A,集合B={x|x2﹣a<0}
(1)求UA;
(2)若A∪B=A,求实数a的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
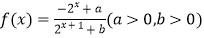 .
.
(1)当a=b=2时,证明:函数f(x)不是奇函数;
(2)设函数f(x)是奇函数,求a与b的值;
(3)在(2)条件下,判断并证明函数f(x)的单调性,并求不等式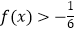 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数
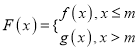 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
相关试题

