【题目】已知函数f(x)=(x2﹣x﹣ ![]() )eax(a>0).
)eax(a>0).
(1)求函数y=f(x)的最小值;
(2)若存在唯一实数x0 , 使得f(x0)+ ![]() =0成立,求实数a的值.
=0成立,求实数a的值.
参考答案:
【答案】
(1)解:函数y=f(x)的定义域为R,f′(x)=[ax2+(2﹣a)x﹣2]eax.
令f′(x)=0,得x=1,x=﹣ ![]() <0,
<0,
当x∈(﹣∞,﹣ ![]() ),(1,+∞)时,f′(x)>0,当x∈(﹣v,1)时,f′(x)<0.
),(1,+∞)时,f′(x)>0,当x∈(﹣v,1)时,f′(x)<0.
∴函数f(x)在(﹣∞,﹣ ![]() ),(1,+∞)上递增,在∈(﹣
),(1,+∞)上递增,在∈(﹣ ![]() ,1)递减.
,1)递减.
注意到x<﹣ ![]() ,x2﹣x﹣
,x2﹣x﹣ ![]() >0,f(1)=﹣
>0,f(1)=﹣ ![]() <0.
<0.
∴函数y=f(x)的最小值为f(1)=﹣ ![]()
(2)解:存在唯一实数x0,使得f(x0)+ ![]() =0成立函数y=f(x)图象与y=﹣
=0成立函数y=f(x)图象与y=﹣ ![]() <(﹣
<(﹣ ![]() 0)有唯一交点,
0)有唯一交点,
结合(1)可得函数f(x)在(﹣∞,﹣ ![]() ),(1,+∞)上递增,在∈(﹣
),(1,+∞)上递增,在∈(﹣ ![]() ,1)递减.
,1)递减.
注意到x<﹣ ![]() ,x2﹣x﹣
,x2﹣x﹣ ![]() >0,f(1)=﹣
>0,f(1)=﹣ ![]() <0.
<0.
∴当且仅当﹣ ![]() 时,存在唯一实数x0,使得f(x0)+
时,存在唯一实数x0,使得f(x0)+ ![]() =0成立,
=0成立,
即a=ln3时,存在唯一实数x0,使得f(x0)+ ![]() =0成立
=0成立
【解析】(1)函数y=f(x)的定义域为R,f′(x)=[ax2+(2﹣a)x﹣2]eax . 利用导数可得函数f(x)在(﹣∞,﹣ ![]() ),(1,+∞)上递增,在∈(﹣
),(1,+∞)上递增,在∈(﹣ ![]() ,1)递减.注意到x<﹣
,1)递减.注意到x<﹣ ![]() ,x2﹣x﹣
,x2﹣x﹣ ![]() >0,f(1)=﹣
>0,f(1)=﹣ ![]() <0.即函数y=f(x)的最小值为f(1)(2)存在唯一实数x0 , 使得f(x0)+
<0.即函数y=f(x)的最小值为f(1)(2)存在唯一实数x0 , 使得f(x0)+ ![]() =0成立函数y=f(x)图象与y=﹣
=0成立函数y=f(x)图象与y=﹣ ![]() <(﹣
<(﹣ ![]() 0)有唯一交点,结合图象且仅当﹣
0)有唯一交点,结合图象且仅当﹣ ![]() 时,存在唯一实数x0 , 使得f(x0)+
时,存在唯一实数x0 , 使得f(x0)+ ![]() =0成立,
=0成立,
即可求得实数a的值.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数y=sin(2x﹣
 )的图象,可以将函数y=sin2x的图象( )
)的图象,可以将函数y=sin2x的图象( )
A.向右平移 个单位
个单位
B.向右平移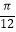 个单位
个单位
C.向左平移 个单位
个单位
D.向左平移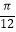 个单位
个单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2eax , a>0.
(1)证明:函数y=f(x)在(0,+∞)上为增函数;
(2)若方程f(x)﹣1=0有且只有两个不同的实数根,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)是否存在实数
 ,使
,使 恒成立,若存在,求出实数
恒成立,若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
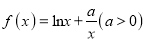 .
.(Ⅰ) 若函数
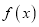 有零点, 求实数
有零点, 求实数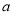 的取值范围;
的取值范围;(Ⅱ) 证明:当
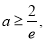 时,
时, 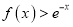
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=2sin(
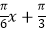 )(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(
)(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则( 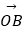 +
+ 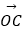 )
) 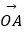 =( )
=( )
A.﹣32
B.﹣16
C.16
D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】直线l与两直线y=1,x﹣y﹣7=0分别交于A,B两点,若直线AB的中点是M(1,﹣1),则直线l的斜率为 .
相关试题

