【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)是否存在实数![]() ,使
,使![]() 恒成立,若存在,求出实数
恒成立,若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
参考答案:
【答案】(1)函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ;
;
(2)当![]() 时,使
时,使![]() 恒成立.
恒成立.
【解析】试题分析:(1)借助题设条件运用导数的知识;(2)借助题设运用导数的知识求解探求.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,
由![]() ,得
,得![]() ,或
,或![]() ,
,
由![]() ,得
,得![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立,
故函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)![]() 恒成立等价于
恒成立等价于![]() 恒成立,
恒成立,
令![]() ,
,
当![]() 时,即当
时,即当![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 内不能恒成立,
内不能恒成立,
当![]() 时,即当
时,即当![]() 时,则
时,则![]() ,
,
故![]() 在
在![]() 内不能恒成立,
内不能恒成立,
当![]() 时,即当
时,即当![]() 时,
时,
![]() ,
,
由![]() 解得
解得![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
所以![]() ,
,
解得![]() .
.
综上,当![]() 时,
时, ![]() 在
在![]() 内恒成立,即
内恒成立,即![]() 恒成立,
恒成立,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
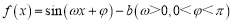 的图像两相邻对称轴之间的距离是
的图像两相邻对称轴之间的距离是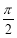 ,若将
,若将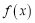 的图像先向右平移
的图像先向右平移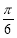 个单位,再向上平移
个单位,再向上平移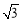 个单位,所得函数
个单位,所得函数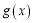 为奇函数.
为奇函数.(1)求
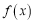 的解析式;
的解析式;(2)求
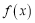 的对称轴及单调区间;
的对称轴及单调区间;(3)若对任意
 ,
,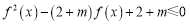 恒成立,求实数
恒成立,求实数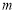 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】由与圆心距离相等的两条弦长相等,想到与球心距离相等的两个截面圆的面积相等,用的是( )
A. 三段论推理 B. 类比推理 C. 归纳推理 D. 传递性关系推理
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
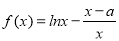 ,其中
,其中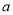 为常数.
为常数.(1)若曲数
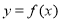 在点
在点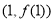 处的切线与直线
处的切线与直线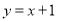 垂直,求函数
垂直,求函数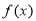 的单调递减区间;
的单调递减区间;(2)若函数
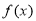 在区间[1,3]上的最小值为
在区间[1,3]上的最小值为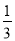 ,求
,求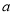 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:
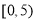 ,
,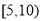 ,
,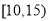 ,
,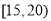 ,
,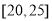 ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:(Ⅰ)写出
 的值;
的值;(Ⅱ)求在抽取的40名学生中月上网次数不少于15次的学生人数;
(Ⅲ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人 ,求至少抽到1名女生
的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
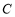 的极坐标方程为
的极坐标方程为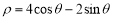 ,直线
,直线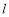 的参数方程为
的参数方程为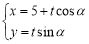 (
(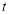 为参数).若直线
为参数).若直线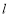 与圆
与圆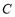 相交于不同的两点
相交于不同的两点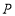 ,
,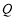 .
.(Ⅰ)写出圆
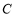 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;(Ⅱ)若弦长
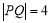 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
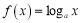 ,
,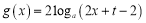 ,其中
,其中 且
且 ,
,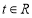 .
.(1)若
 ,且
,且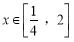 时,
时,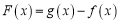 的最小值是
的最小值是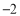 ,求实数
,求实数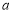 的值;
的值;(2)若
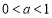 ,且
,且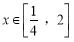 时,有
时,有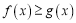 恒成立,求实数
恒成立,求实数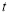 的取值范围.
的取值范围.
相关试题

