【题目】直线l与两直线y=1,x﹣y﹣7=0分别交于A,B两点,若直线AB的中点是M(1,﹣1),则直线l的斜率为 .
参考答案:
【答案】![]()
【解析】解:设直线l的斜率为k,又直线l过M(1,﹣1),则直线l的方程为y+1=k(x﹣1),联立直线l与y=1,得到 ![]() ,
,
解得x= ![]() ,
,
∴A( ![]() ,1);
,1);
联立直线l与x﹣y﹣7=0,得到 ![]() ,
,
解得x= ![]() ,y=
,y= ![]() ,
,
∴B( ![]() ,
, ![]() ),
),
又线段AB的中点M(1,﹣1),
∴ 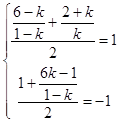 ,解得k=﹣
,解得k=﹣ ![]() .
.
所以答案是: ![]()
【考点精析】根据题目的已知条件,利用直线的斜率的相关知识可以得到问题的答案,需要掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x2﹣x﹣
 )eax(a>0).
)eax(a>0).
(1)求函数y=f(x)的最小值;
(2)若存在唯一实数x0 , 使得f(x0)+ =0成立,求实数a的值.
=0成立,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
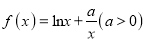 .
.(Ⅰ) 若函数
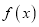 有零点, 求实数
有零点, 求实数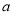 的取值范围;
的取值范围;(Ⅱ) 证明:当
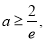 时,
时, 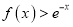
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=2sin(
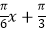 )(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(
)(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则( 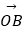 +
+ 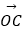 )
) 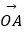 =( )
=( )
A.﹣32
B.﹣16
C.16
D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,  是边长为4的正方形.平面
是边长为4的正方形.平面 ⊥平面
⊥平面 ,
,  .
.(1)求证:
 ⊥平面ABC;
⊥平面ABC;(2)求二面角
 的余弦值;
的余弦值;(3)证明:在线段
 存在点
存在点 ,使得
,使得 ,并求
,并求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果x与y都是整数,就称点(x,y)为整点,下列命题中正确的是(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②如果k与b都是无理数,则直线y=kx+b不经过任何整点;
③如果直线l经过两个不同的整点,则直线l必经过无穷多个整点;
④直线y=kx+b经过无穷多个整点的充分必要条件是:k与b都是有理数;
⑤存在恰经过一个整点的直线.
相关试题

