【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点O为极点,
,(t为参数),在以原点O为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 两点的极坐标分别为.
两点的极坐标分别为.![]()
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最小值.
面积的最小值.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)4
;(2)4
【解析】试题分析:(1)由圆C的参数方程消去t得到圆C的普通方程,由直线l的极坐标方程,利用两角和与差的余弦函数公式化简,根据![]() 转化为直角坐标方程即可;(2)将A与B的极坐标化为直角坐标,并求出|AB|的长,根据P在圆C上,设出P坐标,利用点到直线的距离公式表示出P到直线l的距离,利用余弦函数的值域确定出最小值,即可确定出三角形PAB面积的最小值.
转化为直角坐标方程即可;(2)将A与B的极坐标化为直角坐标,并求出|AB|的长,根据P在圆C上,设出P坐标,利用点到直线的距离公式表示出P到直线l的距离,利用余弦函数的值域确定出最小值,即可确定出三角形PAB面积的最小值.
试题解析:
(1)由![]() 消去参数t,得
消去参数t,得![]() ,
,
所以圆C的普通方程为![]() .
.
由![]() ,得
,得![]() ,换成直角坐标系为
,换成直角坐标系为![]() ,
,
所以直线l的直角坐标方程为![]()
(2)![]() 化为直角坐标为
化为直角坐标为![]() 在直线l上,
在直线l上,
并且![]() ,设P点的坐标为
,设P点的坐标为![]() ,
,
则P点到直线l的距离为![]() ,
,
![]() ,所经
,所经![]() 面积的最小值是
面积的最小值是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:

(参考公式和计算结果:
 ,
,  ,
,  ,
,  )
)(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为
 ,求
,求 的值,并估计
的值,并估计 的预报值.
的预报值.(2)现准备勘探新井
 ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的 ,
,  的值(
的值( ,
,  精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的 ,
,  ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井 ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?(3)设出油量与勘探深度的比值
 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
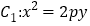 的焦点在抛物线
的焦点在抛物线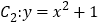 上,点
上,点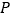 是抛物线
是抛物线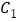 上的动点.
上的动点.(1)求抛物线
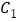 的方程及其准线方程;
的方程及其准线方程;(2)过点
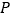 作抛物线
作抛物线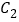 的两条切线,
的两条切线, 、
、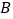 分别为两个切点,求
分别为两个切点,求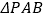 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
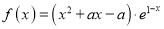 ,其中
,其中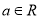 .
.(Ⅰ)求函数
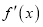 的零点个数;
的零点个数;(Ⅱ)证明:
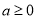 是函数
是函数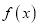 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件. -
科目: 来源: 题型:
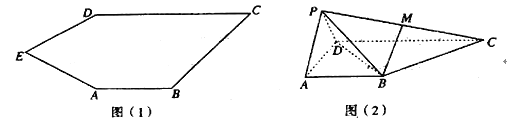
查看答案和解析>>【题目】如图(1),五边形
 中,
中, 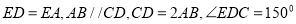 .如图(2),将
.如图(2),将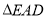 沿
沿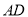 折到
折到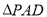 的位置,得到四棱锥
的位置,得到四棱锥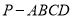 .点
.点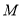 为线段
为线段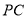 的中点,且
的中点,且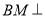 平面
平面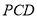 .
.
(1)求证:平面
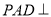 平面
平面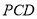 ;
;(2)若直线
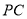 与
与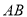 所成角的正切值为
所成角的正切值为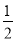 ,设
,设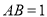 ,求四棱锥
,求四棱锥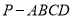 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动.“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车……”铿锵有力的话语,传递了绿色出行、低碳生活的理念.
某机构随机调查了本市部分成年市民某月骑车次数,统计如下:

 人数 次数
人数 次数年龄
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60]
18岁至31岁
8
12
20
60
140
150
32岁至44岁
12
28
20
140
60
150
45岁至59岁
25
50
80
100
225
450
60岁及以上
25
10
10
18
5
2
联合国世界卫组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.用样本估计总体的思想,解决如下问题:
(1)估计本市一个18岁以上青年人每月骑车的平均次数;
(2)若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
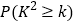
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的顶点是原点,以
的顶点是原点,以 轴为对称轴,且经过点
轴为对称轴,且经过点 .
.(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)设点
 ,
, 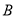 在抛物线
在抛物线 上,直线
上,直线 ,
,  分别与
分别与 轴交于点
轴交于点 ,
,  ,
,  .求直线
.求直线 的斜率.
的斜率.
相关试题

