【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点是原点,以
的顶点是原点,以![]() 轴为对称轴,且经过点
轴为对称轴,且经过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() ,
, ![]() .求直线
.求直线![]() 的斜率.
的斜率.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)利用待定系数法,将点![]() 代入即可得到抛物线
代入即可得到抛物线![]() 的方程;(Ⅱ)由
的方程;(Ⅱ)由![]() ,得直线
,得直线![]() 与
与![]() 的倾斜角互补,所以
的倾斜角互补,所以 ![]() ,设出直线
,设出直线![]() 的方程与抛物线联立可得
的方程与抛物线联立可得![]() 点坐标,将
点坐标,将![]() 换为
换为![]() 可得
可得![]() 点坐标,由两点间斜率计算公式可得结果.
点坐标,由两点间斜率计算公式可得结果.
试题解析:(Ⅰ)

依题意,设抛物线![]() 的方程为
的方程为![]() .由抛物线
.由抛物线![]() 且经过点
且经过点![]() ,得
,得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(Ⅱ)因为![]() ,所以
,所以![]() ,
,
所以 ![]() ,所以 直线
,所以 直线![]() 与
与![]() 的倾斜角互补,所以
的倾斜角互补,所以 ![]() .
.
依题意,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为: ![]() ,
,
将其代入抛物线![]() 的方程,整理得
的方程,整理得![]() .
.
设![]() ,则
,则 ![]() ,
, ![]() ,
,
所以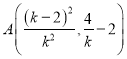 .以
.以![]() 替换点
替换点![]() 坐标中的
坐标中的![]() ,得
,得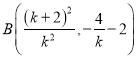 .
.
所以 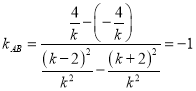 .所以直线
.所以直线![]() 的斜率为
的斜率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以
 为组距分成
为组距分成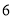 组:
组: 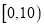 ,
, 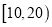 ,
, 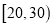 ,
, 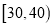 ,
, 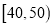 ,
, 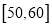 ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表: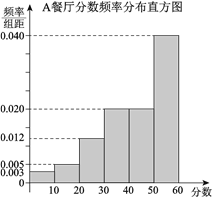
B餐厅分数频数分布表
分数区间
频数
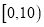
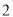
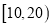
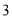
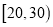
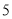
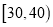
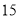
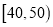
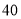
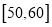
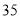
定义学生对餐厅评价的“满意度指数”如下:
分数
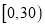
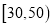
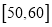
满意度指数
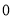
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为
 的人数;
的人数;(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,直线
,直线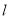 :
: 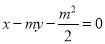 ,椭圆
,椭圆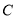 :
: 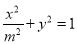 ,
,  、
、 分别为椭圆
分别为椭圆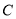 的左、右焦点.
的左、右焦点.(1)当直线
 过右焦点
过右焦点 时,求直线
时,求直线 的方程;
的方程;(2)设直线
 与椭圆
与椭圆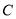 交于
交于 ,
,  两点,
两点,  ,
,  的重心分别为
的重心分别为 ,
,  ,若原点
,若原点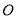 在以线段
在以线段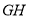 为直径的圆内,求实数
为直径的圆内,求实数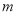 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
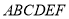 中,底面
中,底面 为矩形,
为矩形, 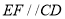 ,
, 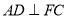 .点
.点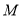 在棱
在棱 上,平面
上,平面 与棱
与棱 交于点
交于点 .
.(Ⅰ)求证:
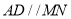 ;
;(Ⅱ)求证:平面
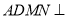 平面
平面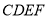 ;
;(Ⅲ)若
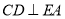 ,
, 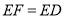 ,
, 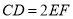 ,平面
,平面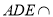 平面
平面 ,求二面角
,求二面角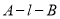 的大小.
的大小.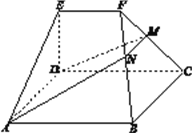
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
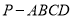 中,底面
中,底面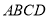 为梯形,
为梯形, 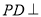 底面
底面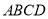 ,
, 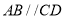 ,
, 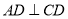 ,
, 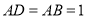 ,
, 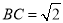 .
. 
(1)求证:平面
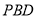
 平面
平面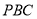 ;
;(2)设
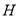 为
为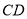 上的一点,满足
上的一点,满足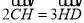 ,若直线
,若直线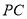 与平面
与平面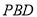 所成角的正切值为
所成角的正切值为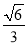 ,求二面角
,求二面角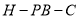 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等差数列,满足
是等差数列,满足 ,
,  ,数列
,数列 满足
满足 ,
,  ,且
,且 是等比数列.
是等比数列.(1)求数列
 和
和 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和.
项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 :
: 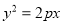 与椭圆
与椭圆 :
: 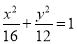 在第一象限的交点为
在第一象限的交点为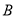 ,
, 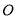 为坐标原点,
为坐标原点, 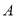 为椭圆的右顶点,
为椭圆的右顶点, 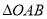 的面积为
的面积为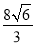 .
.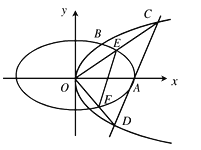
(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)过
 点作直线
点作直线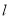 交
交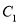 于
于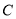 、
、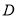 两点,射线
两点,射线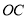 、
、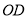 分别交
分别交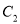 于
于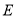 、
、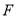 两点,记
两点,记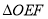 和
和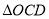 的面积分别为
的面积分别为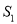 和
和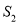 ,问是否存在直线
,问是否存在直线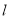 ,使得
,使得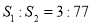 ?若存在,求出直线
?若存在,求出直线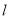 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
相关试题

