【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)求函数![]() 的零点个数;
的零点个数;
(Ⅱ)证明: ![]() 是函数
是函数![]() 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件.
参考答案:
【答案】(I)详见解析;(II)详见解析.
【解析】试题分析:(Ⅰ)对函数![]() 求导有
求导有![]() ,令
,令![]() ,求出根,得到
,求出根,得到![]() 的零点个数,注意分情况讨论;(Ⅱ)根据(Ⅰ)的分类讨论,分别利用导数与函数最值的关系以及充分不必要条件的定义即可证明.
的零点个数,注意分情况讨论;(Ⅱ)根据(Ⅰ)的分类讨论,分别利用导数与函数最值的关系以及充分不必要条件的定义即可证明.
试题解析:
(Ⅰ)由![]() ,
,
得![]()
![]()
![]()
令![]() ,得
,得![]() ,或
,或![]() .
.
所以当![]() 时,函数
时,函数![]() 有且只有一个零点:
有且只有一个零点: ![]() ;当
;当![]() 时,函数
时,函数![]() 有两个相异的零点:
有两个相异的零点: ![]() ,
, ![]() .
.
(Ⅱ)①当![]() 时,
时, ![]() 恒成立,此时函数
恒成立,此时函数![]() 在
在![]() 上单调递减,
上单调递减,
所以,函数![]() 无极值.
无极值.
②当![]() 时,
时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:

所以, ![]() 时,
时, ![]() 的极小值为
的极小值为![]() .
.
又![]() 时,
时, ![]() ,
,
所以,当![]() 时,
时, ![]() 恒成立.
恒成立.
所以, ![]() 为
为![]() 的最小值.
的最小值.
故![]() 是函数
是函数![]() 存在最小值的充分条件.
存在最小值的充分条件.
③当![]() 时,
时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:

因为当![]() 时,
时, ![]() ,
,
又![]() ,
,
所以,当![]() 时,函数
时,函数![]() 也存在最小值.
也存在最小值.
所以, ![]() 不是函数
不是函数![]() 存在最小值的必要条件.
存在最小值的必要条件.
综上, ![]() 是函数
是函数![]() 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件.
点睛; 本题注意考查了导数与函数的极值、最值的关系,属于中档题. 涉及的考点有:用导数研究函数的极值、最值,充分不必要条件的判断,根的存在及个数判断. 考查了学生分析问题和转化的能力以及分类讨论思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对边分别为a,b,c且acosC,bcosB,ccosA成等差数列.
(1)求B的值;
(2)求2sin2A﹣1+cos(A﹣C)的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有三支股票
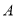 ,
,  ,
,  ,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有
,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有 股票的人中,持有
股票的人中,持有 股票的人数是持有
股票的人数是持有 股票的人数的2倍.在持有
股票的人数的2倍.在持有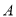 股票的人中,只持有
股票的人中,只持有 股票的人数比除了持有
股票的人数比除了持有 股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有
股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有 股票.则只持有
股票.则只持有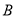 股票的股民人数是( )
股票的股民人数是( )A.
 B.
B. 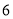 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
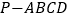 中,
中,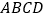 是边长为
是边长为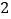 的棱形,且
的棱形,且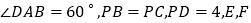 分别是
分别是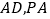 的中点.
的中点.(1)证明:
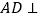 平面
平面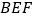 ;
;(2)若二面角
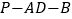 的大小为
的大小为 ,求点
,求点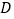 到平面
到平面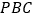 的距离.
的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
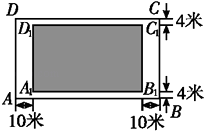
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
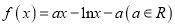 .
.(Ⅰ)讨论函数
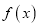 的单调性;
的单调性;(Ⅱ)或
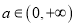 ,
,  时,证明:
时,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为 ,点
,点 .
.(Ⅰ)求椭圆
 的方程.
的方程.(Ⅱ)已知点
 ,是椭圆
,是椭圆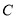 上的两点.
上的两点.(ⅰ)若
 ,且
,且 为等边三角形,求
为等边三角形,求 的面积;
的面积;(ⅱ)若
 ,证明:
,证明:  不可能为等边三角形.
不可能为等边三角形.
相关试题

