【题目】已知函数![]() .
.
(Ⅰ)若![]() 为函数
为函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)讨论![]() 在定义域上的单调性.
在定义域上的单调性.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ) ①当
;(Ⅱ) ①当![]() 时,
时, ![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;②当
递减;②当![]() 时,若
时,若![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;③当
递减;③当![]() 时,
时, ![]() 在
在![]() 内递减;④当
内递减;④当![]() 时,
时, ![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;
递增;
若![]() ,
, ![]() 递减.
递减.
【解析】试题分析:
(1)由题意可得![]() ,解得
,解得![]() .注意检验a的正确性.
.注意检验a的正确性.
(2)导函数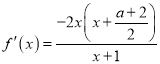 ,分类讨论可得:
,分类讨论可得:
①当![]() 时,
时, ![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;
递减;
②当![]() 时,若
时,若![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减;
递减;
③当![]() 时,
时, ![]() 在
在![]() 内递减;
内递减;
④当![]() 时,
时, ![]() ,
, ![]() 递减;若
递减;若![]() ,
, ![]() 递增;若
递增;若![]() ,
, ![]() 递减.
递减.
试题解析:
(Ⅰ)因为![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() .
.
经检验:当![]() 时,
时, ![]() 递增;
递增;
当![]() 时,
时, ![]() 递减.
递减.
所以![]() 在
在![]() 处取最大值.
处取最大值.
所以![]() 满足题意.
满足题意.
(Ⅱ) 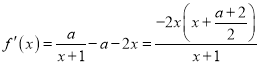 ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
又![]() 的定义域为
的定义域为![]() .
.
①当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减;
递减;
②当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递减;
递减;
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减;
递减;
③当![]() ,即
,即![]() 时,
时,
![]() ,
, ![]() 在
在![]() 内递减;
内递减;
④当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 递减;
递减;
若![]() ,则
,则![]() 递增;
递增;
若![]() ,则
,则![]() 递减.
递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】销售甲、乙两种商品所得利润分别是P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式P=3
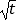 ,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)怎样将资金分配给甲、乙两种商品,能使得总利润y达到最大值,最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax﹣1(a>0,且a≠1).
(1)求f(2)+f(﹣2)的值;
(2)求f(x)的解析式;
(3)解关于x的不等式f(x)<4,结果用集合或区间表示. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)已知抛物线
 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为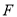 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为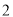 ,且
,且 .
.(Ⅰ)求此抛物线
 的方程;
的方程;(Ⅱ)过点
 做直线
做直线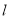 交抛物线
交抛物线 于
于 两点,求证:
两点,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
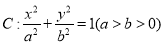 的左、右焦点分别为
的左、右焦点分别为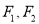 ,离心率为
,离心率为 ,点
,点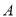 是椭圆上任意一点,
是椭圆上任意一点, 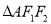 的周长为
的周长为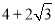 .
.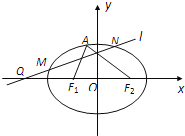
(Ⅰ)求椭圆
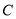 的方程;
的方程;(Ⅱ)过点
 (-4,0)任作一动直线
(-4,0)任作一动直线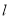 交椭圆
交椭圆 于
于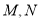 两点,记
两点,记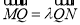 ,若在线段
,若在线段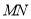 上取一点
上取一点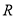 ,使得
,使得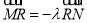 ,则当直线
,则当直线 转动时,点
转动时,点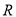 在某一定直线上运动,求该定直线的方程.
在某一定直线上运动,求该定直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( )
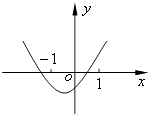
A.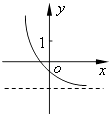
B.
C.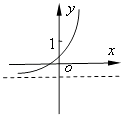
D.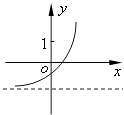
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式的值:
(1) ﹣(
﹣(  )0+(
)0+(  )﹣0.5+
)﹣0.5+  ;
;
(2)lg500+lg ﹣
﹣  lg64+50(lg2+lg5)2 .
lg64+50(lg2+lg5)2 .
相关试题

