【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
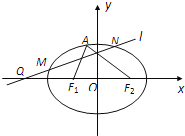
(Ⅱ)过点![]() (-4,0)任作一动直线
(-4,0)任作一动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,记
两点,记![]() ,若在线段
,若在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,则当直线
,则当直线![]() 转动时,点
转动时,点![]() 在某一定直线上运动,求该定直线的方程.
在某一定直线上运动,求该定直线的方程.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ) 点
;(Ⅱ) 点![]() 在定直线
在定直线![]() 上.
上.
【解析】试题分析: (1)由已知条件求出![]() 的值, 根据
的值, 根据![]() ,求出椭圆的方程; (2)设直线
,求出椭圆的方程; (2)设直线![]() 联立直线与椭圆方程, 求出
联立直线与椭圆方程, 求出![]() 的表达式,将
的表达式,将![]() 由
由![]() 表示出来,由
表示出来,由![]() ,求出
,求出![]() 的表达式,化简,求出为定值.
的表达式,化简,求出为定值.
试题解析: (Ⅰ)因为![]() 的周长为
的周长为![]() ,
,
所以![]() ,即
,即![]() .
.
又离心率![]() ,解得
,解得![]() ,
,
![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意可知,直线![]() 的斜率必存在.
的斜率必存在.
故可设直线![]() 的方程为
的方程为![]() ,
,
由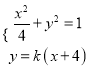 ,消去
,消去![]() 得
得![]() ,
,
由根与系数的关系得![]() ,
,
由![]() ,得
,得![]()
所以![]() .
.
所以![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,
解得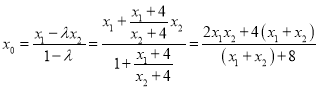 .
.
而![]() ,
,
![]() ,
,
所以![]() .
.
故点![]() 在定直线
在定直线![]() 上.
上.
点睛: 本题主要考查了以椭圆为载体,求椭圆标准方程以及椭圆与直线的关系 ,属于中档题. 考点有: 椭圆的标准方程,椭圆的简单几何性质,韦达定理,向量坐标运算等等. 考查学生的逻辑思维能力,运算求解能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax﹣1(a>0,且a≠1).
(1)求f(2)+f(﹣2)的值;
(2)求f(x)的解析式;
(3)解关于x的不等式f(x)<4,结果用集合或区间表示. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)已知抛物线
 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为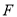 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为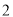 ,且
,且 .
.(Ⅰ)求此抛物线
 的方程;
的方程;(Ⅱ)过点
 做直线
做直线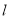 交抛物线
交抛物线 于
于 两点,求证:
两点,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;(Ⅱ)讨论
 在定义域上的单调性.
在定义域上的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( )
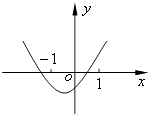
A.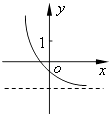
B.
C.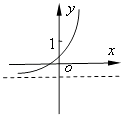
D.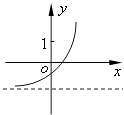
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式的值:
(1) ﹣(
﹣(  )0+(
)0+(  )﹣0.5+
)﹣0.5+  ;
;
(2)lg500+lg ﹣
﹣  lg64+50(lg2+lg5)2 .
lg64+50(lg2+lg5)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|(x﹣a)[x﹣(a+3)]≤0}(a∈R),B={x|x2﹣4x﹣5>0}.
(1)若A∩B=,求实数a的取值范围;
(2)若A∪B=B,求实数a的取值范围.
相关试题

