【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax﹣1(a>0,且a≠1).
(1)求f(2)+f(﹣2)的值;
(2)求f(x)的解析式;
(3)解关于x的不等式f(x)<4,结果用集合或区间表示.
参考答案:
【答案】
(1)解:∵f(x)是R上的奇函数,∴f(﹣2)=﹣f(2),即f(2)+f(﹣2)=0
(2)解:设x<0,则﹣x>0,∴f(﹣x)=a﹣x﹣1.
由f(x)是奇函数,有f(﹣x)=﹣f(x),∵f(﹣x)=a﹣x﹣1,
∴f(x)=﹣a﹣x+1(x<0),∴所求的解析式为 ![]()
(3)解:不等式等价于 ![]() ,
,
即 ![]() ,即
,即 ![]() .
.
当a>1时,有 ![]() ,∵loga5>0,所以不等式的解集为(﹣∞,loga5);
,∵loga5>0,所以不等式的解集为(﹣∞,loga5);
当0<a<1时,有 ![]() ,∵loga5<0,所以不等式的解集为(﹣∞,0).
,∵loga5<0,所以不等式的解集为(﹣∞,0).
综上所述,当a>1时,不等式的解集为(﹣∞,loga5);
当0<a<1时,不等式的解集为(﹣∞,0)
【解析】(1)根据题意可得f(﹣2)=﹣f(2),即f(2)+f(﹣2)=0.(2)设x<0,则﹣x>0,根据f(﹣x)=a﹣x﹣1=﹣f(x),求得f(x)的解析式.(3)分类讨论a的范围,利用函数的单调性求得不等式f(x)<4的解集.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
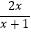 .
.
(1)判断函数f(x)在区间[1,+∞)上的单调性,并用定义证明你的结论;
(2)求函数f(x)在区间[2,4]上的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,点
的焦点重合,点 在
在 上
上(Ⅰ)求
 的方程;
的方程; (Ⅱ)直线
 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴, 与
与 有两个交点
有两个交点 ,线段
,线段 的中点为
的中点为 ,证明:
,证明: 的斜率与直线
的斜率与直线 的斜率的乘积为定值.
的斜率的乘积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】销售甲、乙两种商品所得利润分别是P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式P=3
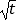 ,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)怎样将资金分配给甲、乙两种商品,能使得总利润y达到最大值,最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)已知抛物线
 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为 轴,焦点为
轴,焦点为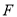 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为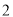 ,且
,且 .
.(Ⅰ)求此抛物线
 的方程;
的方程;(Ⅱ)过点
 做直线
做直线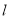 交抛物线
交抛物线 于
于 两点,求证:
两点,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;(Ⅱ)讨论
 在定义域上的单调性.
在定义域上的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
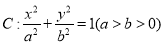 的左、右焦点分别为
的左、右焦点分别为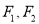 ,离心率为
,离心率为 ,点
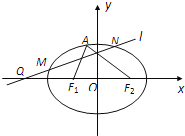
,点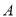 是椭圆上任意一点,
是椭圆上任意一点, 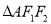 的周长为
的周长为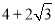 .
.
(Ⅰ)求椭圆
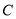 的方程;
的方程;(Ⅱ)过点
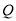 (-4,0)任作一动直线
(-4,0)任作一动直线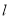 交椭圆
交椭圆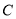 于
于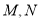 两点,记
两点,记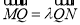 ,若在线段
,若在线段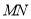 上取一点
上取一点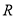 ,使得
,使得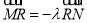 ,则当直线
,则当直线 转动时,点
转动时,点 在某一定直线上运动,求该定直线的方程.
在某一定直线上运动,求该定直线的方程.
相关试题

