【题目】如图,已知椭圆的中心在原点,焦点在![]() 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点![]() ,平行于
,平行于![]() 的直线
的直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 两个不同点.
两个不同点.

(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)-2<m<2,且m≠0
(2)-2<m<2,且m≠0
【解析】
试题分析:(1)设出椭圆的方程,利用长轴长是短轴长的2倍且经过点M(2,1),建立方程,求出a,b,即可求椭圆的方程;(2)由直线方程代入椭圆方程,利用根的判别式,即可求m的取值范围
试题解析:(1)设椭圆方程为![]() (a>b>0)
(a>b>0)
则 解得
解得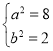
∴椭圆方程为![]()
(2)∵直线l平行于OM,且在y轴上的截距为m
又KOM=![]() ,∴l的方程为:y=
,∴l的方程为:y=![]() x+m
x+m
由 ∴x2+2mx+2m2-4=0
∴x2+2mx+2m2-4=0
∵直线l与椭圆交于A、B两个不同点,
∴Δ=(2m)2-4(2m2-4)>0,
解得-2<m<2,且m≠0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 称为
称为 ,
, 的二维平方平均数,
的二维平方平均数,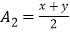 称为
称为 ,
, 的二维算术平均数,
的二维算术平均数, 称为
称为 ,
, 的二维几何平均数,
的二维几何平均数, 称为
称为 ,
, 的二维调和平均数,其中
的二维调和平均数,其中 ,
, 均为正数.
均为正数.(1)试判断
 与
与 的大小,并证明你的猜想.
的大小,并证明你的猜想.(2)令
 ,
, ,试判断
,试判断 与
与 的大小,并证明你的猜想.
的大小,并证明你的猜想.(3)令
 ,
, ,
, ,试判断
,试判断 、
、 、
、 三者之间的大小关系,并证明你的猜想.
三者之间的大小关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
,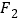 是双曲线C:
是双曲线C: 的左,右焦点,O是坐标原点
的左,右焦点,O是坐标原点 过
过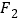 作C的一条渐近线的垂线,垂足为P,若
作C的一条渐近线的垂线,垂足为P,若 ,则C的离心率为
,则C的离心率为

A.
 B. 2 C.
B. 2 C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,其中实数
,其中实数 满足
满足 ,若
,若 的最大值为
的最大值为 ,则
,则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
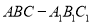 中,侧棱
中,侧棱 底面
底面 ,
,  为棱
为棱 中点.
中点. 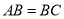 ,
,  ,
,  .
.
(I)求证:
 平面
平面 .
.(II)求证:
 平面
平面 .
.(III)在棱
 的上是否存在点
的上是否存在点 ,使得平面
,使得平面 平面
平面 ?如果存在,求此时
?如果存在,求此时 的值;如果不存在,说明理由.
的值;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解关于x的不等式

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.

(1)求
 的值;
的值;(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
相关试题

