【题目】设函数![]() .
.
(1)当![]() 时,函数
时,函数![]() 与
与![]() 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数![]() 的范围;
的范围;
(2)讨论![]() 的单调性.
的单调性.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,函数在
时,函数在![]() 上单调递减,当
上单调递减,当![]() 时,函数在
时,函数在![]() 上递减,在
上递减,在![]() 上递增,在
上递增,在![]() 上递减,当
上递减,当![]() 时,函数在
时,函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
【解析】
试题分析:本题考查利用导数研究函数的单调性、函数的极值与零点个数以及分类讨论思想的应用;(1)作差,分离参数构造函数,通过导数研究函数的极值,再通过函数的图象进行求解;(2)求导,确定导函数的两个零点,讨论两零点的大小进行求解.
试题解析:(1)当![]() 时,
时, ![]() ,
,
故![]() ,令
,令![]() ,
,
则![]() ,
,
故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;![]() ,
,![]() ,故
,故![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() 恒成立,故函数
恒成立,故函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,在
上递增,在![]() 上递减;当
上递减;当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,函数在
时,函数在![]() 上单调递减,当
上单调递减,当![]() 时,函数在
时,函数在![]() 上递减,在
上递减,在![]() 上递增,在
上递增,在![]() 上递减;当
上递减;当![]() 时,函数在
时,函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
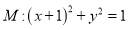 ,圆
,圆 ,动圆
,动圆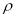 与圆
与圆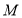 外切并与圆
外切并与圆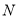 内切,圆心
内切,圆心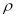 的轨迹为曲线
的轨迹为曲线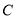 .
.(1)求
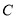 的方程;
的方程;(2)
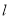 是与圆
是与圆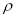 ,圆
,圆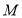 都相切的一条直线,
都相切的一条直线,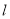 与曲线
与曲线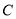 交于
交于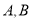 两点,当圆
两点,当圆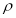 的半径最长时,求
的半径最长时,求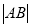 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)若函数
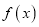 的值域为
的值域为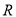 ,求实数
,求实数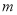 的取值范围;
的取值范围;(2)若函数
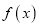 在区间
在区间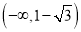 上是减函数,求实数
上是减函数,求实数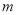 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=(m2-5m+1)xm+1为幂函数,且为奇函数.
(I)求m的值;
(II)求函数g(x)=h(x)+
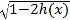 ,x∈
,x∈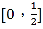 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4
 4:坐标系与参数方程
4:坐标系与参数方程在直角坐标系
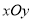 中,直线
中,直线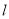 经过点
经过点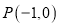 ,其倾斜角为
,其倾斜角为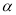 ,在以原点
,在以原点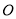 为极点,
为极点, 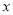 轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为
轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为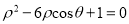 .
.
(Ⅰ)若直线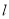 与曲线C有公共点,求
与曲线C有公共点,求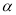 的取值范围;
的取值范围;(Ⅱ)设
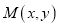 为曲线C上任意一点,求
为曲线C上任意一点,求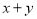 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x).当0≤x≤1时,f(x)=x2.若直线y=x+a与函数y=f(x)的图象有两个不同的公共点,则实数a的值为( )
A. n(n∈Z) B. 2n(n∈Z)
C. 2n或
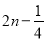 (n∈Z) D. n或
(n∈Z) D. n或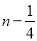 (n∈Z)
(n∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
相关试题

